题目内容
10.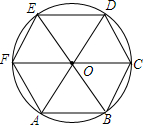 如图所示,△OAB为正三角形,以点O为圆心,OA为半径作⊙O,直径FC∥AB,AO,BO的延长线分别交⊙O于点D,E.
如图所示,△OAB为正三角形,以点O为圆心,OA为半径作⊙O,直径FC∥AB,AO,BO的延长线分别交⊙O于点D,E.求证:六边形ABCDEF是正六边形.
分析 由正三角形的性质得出∠AOB=∠OAB=∠OBA=60°,由平行线的性质得出圆心角相等∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF,由圆心角、弧、弦的关系定理得出弧相等、弦相等,再由圆周角定理证出∠BAF=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,即可得出结论.
解答 证明:∵△OAB是正三角形,
∴∠AOB=∠OAB=∠OBA=60°,
∵FC∥AB,
∴∠AOF=∠A=60°,∠BOC=∠B=60°,
∴∠DOE=∠AOB=60°,∠COD=∠AOF=60°,∠EOF=∠BOC=60°,
∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF,
∴$\widehat{AB}=\widehat{BC}=\widehat{CD}=\widehat{DE}=\widehat{EF}=\widehat{AF}$,AB=BC=CD=DE=EF=AF,
∴$\widehat{BDF}=\widehat{CDA}=\widehat{DEB}=\widehat{EFC}$=$\widehat{FAD}=\widehat{ABE}$,
∴∠BAF=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA,
∴六边形ABCDEF是正六边形.
点评 本题考查了正六边形和圆、正三角形的性质、圆心角、弧、弦的关系定理,圆周角定理;本题综合性强,运用圆心角、弧、弦的关系定理和圆周角定理是解决问题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
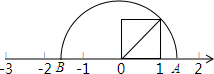 (1)如图,数轴上的A、B两点筏示的数分别是什么?为什么?
(1)如图,数轴上的A、B两点筏示的数分别是什么?为什么?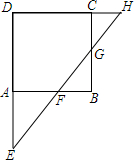 在正方形ABCD中,已知$\frac{AF}{AB}=\frac{1}{3}$,$\frac{CG}{CB}=\frac{1}{4}$
在正方形ABCD中,已知$\frac{AF}{AB}=\frac{1}{3}$,$\frac{CG}{CB}=\frac{1}{4}$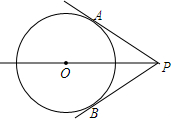 如图,PA,PB是⊙O的两条切线,切点分别为A,B,在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
如图,PA,PB是⊙O的两条切线,切点分别为A,B,在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?