题目内容
15.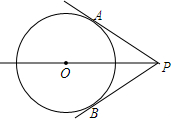 如图,PA,PB是⊙O的两条切线,切点分别为A,B,在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
如图,PA,PB是⊙O的两条切线,切点分别为A,B,在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
分析 根据切线的性质得到∠PAO=∠PBO=90°,通过Rt△APO≌Rt△BPO,即可得到结论.
解答  解:PA=PB,∠APO=∠BPO,
解:PA=PB,∠APO=∠BPO,
理由:连接AO,BO,
∵PA,PB是⊙O的两条切线,
∴∠PAO=∠PBO=90°,
在Rt△APO与Rt△BPO中,
$\left\{\begin{array}{l}{OA=OB}\\{PO=PO}\end{array}\right.$,
∴Rt△APO≌Rt△BPO,
∴PA=PB,∠APO=∠BPO.
点评 本题考查了切线的性质,全等三角形的判定和性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
5.下列计算正确的是( )
| A. | -33=-27 | B. | (-4)2=-16 | C. | (-$\frac{1}{5}$)3=$\frac{1}{125}$ | D. | (-$\frac{1}{3}$)4=-$\frac{4}{3}$ |
 如图,AD=BC,比较$\widehat{AB}$与$\widehat{CD}$的长度,并证明你的结论.
如图,AD=BC,比较$\widehat{AB}$与$\widehat{CD}$的长度,并证明你的结论.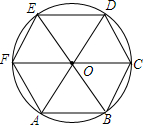 如图所示,△OAB为正三角形,以点O为圆心,OA为半径作⊙O,直径FC∥AB,AO,BO的延长线分别交⊙O于点D,E.
如图所示,△OAB为正三角形,以点O为圆心,OA为半径作⊙O,直径FC∥AB,AO,BO的延长线分别交⊙O于点D,E.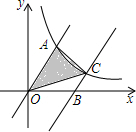 如图,直线y=2x与双曲线y=$\frac{k}{x}$(x>0)相交于点A,过点B(3,0)作直线BC∥0A,交该双曲线于点C,若△0AC的面积是3$\sqrt{3}$,则k的值是6.
如图,直线y=2x与双曲线y=$\frac{k}{x}$(x>0)相交于点A,过点B(3,0)作直线BC∥0A,交该双曲线于点C,若△0AC的面积是3$\sqrt{3}$,则k的值是6. 如图是抛物线y=ax2+bx+c的图象,试根据图中信息,求代数式a2+b的最小值.
如图是抛物线y=ax2+bx+c的图象,试根据图中信息,求代数式a2+b的最小值.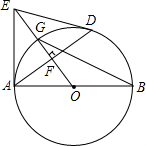 如图,AB是⊙O的直径,D是⊙O上一点,OF⊥AD,过点A作⊙O的切线,交OF的延长线于E.连接DE,DE与⊙O相切,若AE=10,sin∠AEO=$\frac{3}{5}$,求BG长.
如图,AB是⊙O的直径,D是⊙O上一点,OF⊥AD,过点A作⊙O的切线,交OF的延长线于E.连接DE,DE与⊙O相切,若AE=10,sin∠AEO=$\frac{3}{5}$,求BG长.