题目内容
5.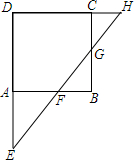 在正方形ABCD中,已知$\frac{AF}{AB}=\frac{1}{3}$,$\frac{CG}{CB}=\frac{1}{4}$
在正方形ABCD中,已知$\frac{AF}{AB}=\frac{1}{3}$,$\frac{CG}{CB}=\frac{1}{4}$求(1)EF:FG:GH,(2)AE:CH.
分析 (1)由正方形的性质得AD∥BC,CD∥AB,再根据平行线分线段成比例定理,由AE∥BG得到$\frac{EF}{FG}$=$\frac{AF}{BF}$,而$\frac{AF}{AB}$=$\frac{1}{3}$,则$\frac{EF}{FG}$=$\frac{1}{2}$,同理可得$\frac{FG}{GH}$=3,然后利用比例性质得到EF:FG:GH=3:6:2;
(2)根据平行线分线段成比例定理和(1)中的结论,由AF∥DH得到$\frac{AE}{AD}$=$\frac{EF}{FH}$=$\frac{3}{8}$,即AE=$\frac{3}{8}$AD,同理可得$\frac{CH}{CD}$=$\frac{GH}{EG}$=$\frac{2}{9}$,即CH=$\frac{2}{9}$CD,根据正方形的性质得AD=CD,所以AE:CH=27:16.
解答 解:(1)∵四边形ABCD为正方形,
∴AD∥BC,CD∥AB,
∵AE∥BG,
∴$\frac{EF}{FG}$=$\frac{AF}{BF}$,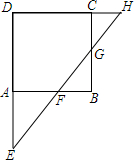
而$\frac{AF}{AB}$=$\frac{1}{3}$,
∴$\frac{AF}{BF}$=$\frac{1}{2}$,
∴$\frac{EF}{FG}$=$\frac{1}{2}$,
∵CH∥BF,
∴$\frac{FG}{GH}$=$\frac{BG}{CG}$,
而$\frac{CG}{BG}$=$\frac{1}{4}$,
∴$\frac{BG}{CG}$=3,
∴$\frac{FG}{GH}$=3,
即$\frac{EF}{FG}$=$\frac{3}{6}$,$\frac{FG}{GH}$=$\frac{6}{2}$,
∴EF:FG:GH=3:6:2;
(2)∵AF∥DH,
∴$\frac{AE}{AD}$=$\frac{EF}{FH}$=$\frac{3}{8}$,即AE=$\frac{3}{8}$AD,
∵CG∥DE,
∴$\frac{CH}{CD}$=$\frac{GH}{EG}$=$\frac{2}{9}$,即CH=$\frac{2}{9}$CD,
而AD=CD,
∴AE:CH=27:16.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了正方形的性质和比例的性质.

| A. | 9 | B. | 18 | C. | 9或18 | D. | 不能确定 |
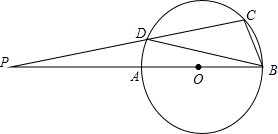 如图,AB是⊙O的直径,点P是BA延长线上一点,PC与⊙O分别交于点D和点C,已知∠P=10°,∠CBD=55°,以BC为边作⊙O的内接正多边形,那么该正多边形是什么?
如图,AB是⊙O的直径,点P是BA延长线上一点,PC与⊙O分别交于点D和点C,已知∠P=10°,∠CBD=55°,以BC为边作⊙O的内接正多边形,那么该正多边形是什么?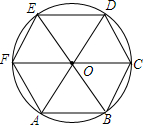 如图所示,△OAB为正三角形,以点O为圆心,OA为半径作⊙O,直径FC∥AB,AO,BO的延长线分别交⊙O于点D,E.
如图所示,△OAB为正三角形,以点O为圆心,OA为半径作⊙O,直径FC∥AB,AO,BO的延长线分别交⊙O于点D,E.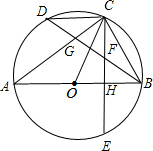 如图,AB是⊙O的直径,BD是弦,C是弧BD的中点,弦CE⊥AB,H是垂足,BD交CE,CA于点F,G.
如图,AB是⊙O的直径,BD是弦,C是弧BD的中点,弦CE⊥AB,H是垂足,BD交CE,CA于点F,G.