题目内容
9.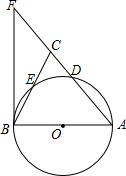 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.(1)求证:∠CBF=$\frac{1}{2}$∠CAB;
(2)连接BD,AE交于点H,若AB=5,tan∠CBF=$\frac{1}{2}$,求BH的值.
分析 (1)连接AE,利用等腰三角形的性质易证∠BAE=∠CAE=$\frac{1}{2}$∠CAB,由弦切角定理可得∠CBD=∠BAE,所以∠CBF=$\frac{1}{2}$∠CAB.
(2)由tan∠CBF=tan∠EAB=$\frac{1}{2}$,得出$\frac{BE}{AE}$=$\frac{1}{2}$,根据勾股定理求得BE,根据圆周角定理得出∠BAE=∠CAE,即可得出∠EBD=∠EAB,由∠EBD=∠EAB,得出tan∠EBD=$\frac{EH}{EB}$=$\frac{1}{2}$,即可求得EH,然后根据勾股定理求得BH即可.
解答 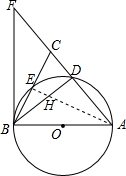 (1)证明:连接AE,
(1)证明:连接AE,
∵AB是圆的直径,
∴AE⊥BC,
∵AB=AC,
∴AE平分∠BAC,
∴∠BAE=∠CAE=$\frac{1}{2}$∠CAB,
∵BF是⊙O的切线,
∴∠CBF=∠BAE,
∴∠CBF=$\frac{1}{2}$∠CAB.
(2)解:∵tan∠CBF=tan∠EAB=$\frac{1}{2}$,
∴$\frac{BE}{AE}$=$\frac{1}{2}$,
∵AB=5,AB2=BE2+AE2,
∴25=BE2+4BE2,
∴BE=$\sqrt{5}$,
∵∠BAE=∠CAE,∠EBD=∠CAE,
∴∠EBD=∠EAB,
∴tan∠EBD=$\frac{EH}{EB}$=$\frac{1}{2}$,
∴EH=$\frac{\sqrt{5}}{2}$,
∴BH=$\sqrt{B{E}^{2}+E{H}^{2}}$=$\frac{5}{2}$.
点评 本题考查了弦切角定理的运用、圆周角定理,勾股定理,直角三角函数以及等腰三角形的性质,解题的关键是正确的添加辅助线,利用等腰三角形的性质解题.

练习册系列答案
相关题目
4.五张完全相同的卡片上,分别写上数字-3,-2,-1,2,3,现从中随机抽取一张,抽到写有负数的卡片的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
14.在3.14、$\sqrt{12}$、$\frac{22}{7}$、-$\sqrt{2}$、$\root{3}{27}$、$\frac{π}{3}$、0.2020020002这六个数中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.在平面直角坐标系中,将点B(-3,2)向右平移5个单位长度,再向下平移3个单位长度后与点A(x,y)重合,则点A的坐标是( )
| A. | (2,5) | B. | (-8,5) | C. | (-8,-1) | D. | (2,-1) |
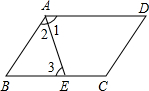 如图所示,在平行四边形ABCD中,∠BAD的平分线AE分对边长度为3和4两部分,求四边形ABCD的周长.
如图所示,在平行四边形ABCD中,∠BAD的平分线AE分对边长度为3和4两部分,求四边形ABCD的周长.