题目内容
14.在3.14、$\sqrt{12}$、$\frac{22}{7}$、-$\sqrt{2}$、$\root{3}{27}$、$\frac{π}{3}$、0.2020020002这六个数中,无理数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 无理数就是无限不循环小数,依据定义即可作出判断.
解答 解:无理数有:$\sqrt{12}$,-$\sqrt{2}$,$\frac{π}{3}$共3个.
故选C.
点评 此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,$\sqrt{6}$,0.8080080008…(每两个8之间依次多1个0)等形式.

练习册系列答案
相关题目
5.在平面直角坐标系中,将点A(-1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C的坐标是( )
| A. | (-4,-2) | B. | (2,2) | C. | (-2,2) | D. | (2,-2) |
3.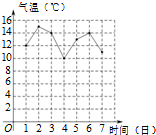 右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )
右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )
 右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )
右图是某市10月1日至7日一周内“日平均气温变化统计图”.在这组数据中,众数和中位数分别是( )| A. | 13,13 | B. | 14,14 | C. | 13,14 | D. | 14,13 |
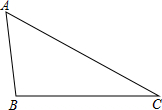 如图,在△ABC中,AB=3,BC=5,AC=6,请解答下列问题:
如图,在△ABC中,AB=3,BC=5,AC=6,请解答下列问题: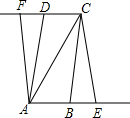 如图,?ABCD中,AB=2cm,AC=5cm,S?ABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒.
如图,?ABCD中,AB=2cm,AC=5cm,S?ABCD=8cm2,E点从B点出发,以1cm每秒的速度,在AB延长线上向右运动,同时,点F从D点出发,以同样的速度在CD延长线上向左运动,运动时间为t秒.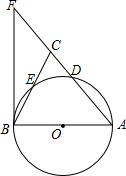 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,过点B作⊙O的切线,交AC的延长线于点F.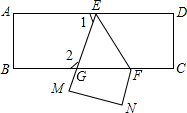 如图已知,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上.若∠EFG=55°,求∠1和∠2的度数.
如图已知,把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上.若∠EFG=55°,求∠1和∠2的度数. 如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE,AE交⊙O于点F.
如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,点E为BC的中点,连接DE、AE,AE交⊙O于点F.