题目内容
12.要使(x2+mx+8)(x2-3x+n)的展开式中不含x3项,且常数项为64,求m,n的值.分析 原式利用多项式乘以多项式法则计算,合并得到结果,由展开式不含x3项,且常数项为64,求出m与n的值即可.
解答 解:原式=x4+(m-3)x3+(n-3m+8)x2+(mn-24)x+8n,
由结果不含x3项,且常数项为64,
得到m-3=0,8n=64,
解得:m=3,n=8.
点评 此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
2.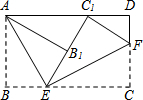 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )| A. | $\sqrt{3}$ | B. | 3 | C. | 2 | D. | 2$\sqrt{3}$ |
4.下列命题中,真命题是( )
| A. | 如果两个角相等,则这两个角是对顶角 | |
| B. | 三角形的角平分线是一条射线 | |
| C. | 互为邻补角的两个角相等 | |
| D. | 同角的余角相等 |
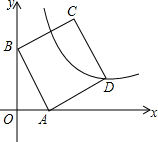 如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为A(1,0),B(0,2),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点D.
如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为A(1,0),B(0,2),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点D.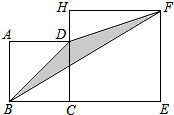 如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为2.
如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为2.