题目内容
3.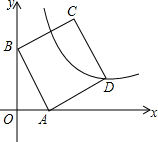 如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为A(1,0),B(0,2),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点D.
如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为A(1,0),B(0,2),反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点D.(1)求反比例函数的解析式;
(2)将正方形ABCD沿x轴向右平移m个单位长度后,使点B落在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,求m的值.
分析 (1)过D作DE垂直于x轴,由A与B的坐标求出OA与OB的长,根据四边形ABCD为正方形,得到AB=AD,且∠BAD为直角,利用同角的余角相等得到一对角相等,利用AAS得到三角形OAB与三角形EDA全等,由全等三角形的对应边相等得到AE=OB=2,DE=OA=1,求出OE的长,确定出D坐标,代入反比例解析式求出k的值即可确定出解析式;
(2)表示出正方形ABCD沿x轴向右平移m个单位长度后B的坐标,代入反比例解析式求出m的值即可.
解答 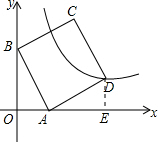 解:(1)过点D作DE⊥x轴于点E,
解:(1)过点D作DE⊥x轴于点E,
∵A(1,0),B(0,2),
∴OA=1,OB=2,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAO+∠DAE=90°,
∵在Rt△ADE中,∠ADE+∠DAE=90°,
∴∠BAO=∠ADE,
在△OAB和△EDA中,
$\left\{\begin{array}{l}{∠BAO=∠ADE}\\{∠AOB=∠DEA}\\{AB=AD}\end{array}\right.$,
∴△OAB≌△EDA(AAS),
∴AE=OB=2,DE=OA=1,
∴OE=3,
∴点D坐标为(3,1),
∵点D在反比例函数y=$\frac{k}{x}$图象上,
∴把D坐标代入反比例解析式得:k=3,
则反比例函数解析式为y=$\frac{3}{x}$;
(2)将正方形ABCD沿x轴向右平移m个单位长度后,点B坐标为(m,2),
把B(m,2)代入y=$\frac{3}{x}$,得:m=$\frac{3}{2}$.
点评 此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,全等三角形的判定与性质,平移的性质,待定系数法确定反比例函数解析式,以及正方形的性质,熟练掌握性质是解本题的关键.

练习册系列答案
相关题目
14.去年我市有56940名初中毕业生参加升学考试,为了了解这56940名考生的数学成绩.从中抽取2000名考生的数学成绩进行统计分析.在这个问题中样本是( )
| A. | 56940名考生 | B. | 所抽取的2000名考生的数学成绩 | ||
| C. | 56940名考生的数学成绩 | D. | 所抽取的2000名考生 |
11.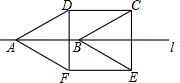 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )| A. | 2cm2 | B. | 3cm2 | C. | 4cm2 | D. | 6cm2 |
13.下列说法正确的是( )
| A. | 6的平方根是±3 | B. | -3是(-3)2的算术平方根 | ||
| C. | $\sqrt{6}$是$\sqrt{36}$的算术平方根 | D. | 8的立方根是±2 |
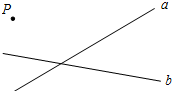 (1)在图中画出表示点P到直线a距离的线段PM;
(1)在图中画出表示点P到直线a距离的线段PM;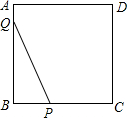 如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为3π.
如图,正方形ABCD,边长为4,点P和点Q在正方形的边上运动,且PQ=4,若点P从点B出发沿B→C→D→A的路线向点A运动,到点A停止运动;点Q从点A出发,沿A→B→C→D的路线向点D运动,到达点D停止运动.它们同时出发,且运动速度相同,则在运动过程中PQ的中点O所经过的路径长为3π.