题目内容
2．
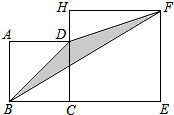如图，正方形ABCD的边长为2，H在CD的延长线上，四边形CEFH也为正方形，则△DBF的面积为2．
分析 设正方形CEFH边长为a，根据S△BDF=S正方形ABCD+S正方形CEFH-S△ABD-S△DHF-S△BEF求解即可．
解答 解：设正方形CEFH的边长为a，根据题意得：
S△BDF=S正方形ABCD+S正方形CEFH-S△ABD-S△DHF-S△BEF
=4+a2-$\frac{1}{2}$×4-$\frac{1}{2}$a（a-2）-$\frac{1}{2}$a（a+2）
=2+a2-$\frac{1}{2}$a2+a-$\frac{1}{2}$a2-a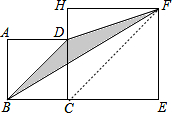
=2．
故答案为：2．
方法二：连接CF．易证BD∥CF，
∴S△BDF=S△BDC=$\frac{1}{2}$S正方形ABCD=2．
点评 此题考查了正方形的性质，正确的列出阴影部分的面积式子是解本题的关键．
练习册系列答案
相关题目
13．下列说法正确的是（ ）
| A． | 6的平方根是±3 | B． | -3是（-3）2的算术平方根 | ||
| C． | $\sqrt{6}$是$\sqrt{36}$的算术平方根 | D． | 8的立方根是±2 |
10．下列等式成立的是（ ）
| A． | $\sqrt{{a}^{2}+{b}^{2}}$=a+b | B． | $\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$ | C． | $\sqrt{\frac{a}{b}}$=$\frac{\sqrt{a}}{\sqrt{b}}$ | D． | $\sqrt{-{a}^{2}{b}^{2}}$=0 |
17．一次函数y=2x-4的图象与y轴交点的坐标是（ ）
| A． | （0，4） | B． | （0，-4） | C． | （2，0） | D． | （-2，0） |
7．分式$\frac{x+1}{x-2}$无意义，则x的取值是（ ）
| A． | x≠2 | B． | x≠-1 | C． | x=2 | D． | x=-1 |
11．下列四种调查中，适合用普查的是（ ）
| A． | 了解某市所有八年级学生的视力状况 | |
| B． | 了解中小学生的主要娱乐方式 | |
| C． | 登飞机前，对旅客进行安全检查 | |
| D． | 估计某水库中每条鱼的平均重量 |