题目内容
1.已知关于x的函数y=(n+1)${x}^{{n}^{2}-n}$-3x+2(x≠0),当n为何值时(1)函数是一次函数?
(2)函数是二次函数?
分析 根据形如y=kx+b (k≠0)是一次函数,可得答案;
形如y=ax2+bx+c (a≠0)二次函数,可得答案.
解答 解:(1)根据一次函数的定义,得:$\left\{\begin{array}{l}{{n}^{2}-n=1}\\{n+1≠3}\end{array}\right.$,
解得n=$\frac{1±\sqrt{5}}{2}$;
n2-n=0,解得n=0或n=1;
又∵n+1=0即n=-1;
∴当n=$\frac{1±\sqrt{5}}{2}$或n=0或n=1或n=-1时,这个函数是一次函数;
(2)根据二次函数的定义,得:$\left\{\begin{array}{l}{{n}^{2}-n=2}\\{n+1≠0}\end{array}\right.$,
解得n=2,
故当n=2时,这个函数是二次函数.
点评 本题考查了二次函数的定义,解题关键是掌握一次函数与二次函数的定义.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
11.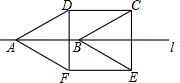 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )| A. | 2cm2 | B. | 3cm2 | C. | 4cm2 | D. | 6cm2 |
13.下列说法正确的是( )
| A. | 6的平方根是±3 | B. | -3是(-3)2的算术平方根 | ||
| C. | $\sqrt{6}$是$\sqrt{36}$的算术平方根 | D. | 8的立方根是±2 |
10.下列等式成立的是( )
| A. | $\sqrt{{a}^{2}+{b}^{2}}$=a+b | B. | $\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$ | C. | $\sqrt{\frac{a}{b}}$=$\frac{\sqrt{a}}{\sqrt{b}}$ | D. | $\sqrt{-{a}^{2}{b}^{2}}$=0 |
11.下列四种调查中,适合用普查的是( )
| A. | 了解某市所有八年级学生的视力状况 | |
| B. | 了解中小学生的主要娱乐方式 | |
| C. | 登飞机前,对旅客进行安全检查 | |
| D. | 估计某水库中每条鱼的平均重量 |