题目内容
2.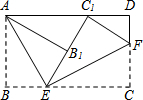 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=$\sqrt{3}$,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )| A. | $\sqrt{3}$ | B. | 3 | C. | 2 | D. | 2$\sqrt{3}$ |
分析 由三角函数易得BE,AE长,根据翻折和对边平行可得△AEC1和△CEC1为等边三角形,那么就得到EC长,相加即可.
解答  解:连接CC1.
解:连接CC1.
在Rt△ABE中,∠BAE=30°,AB=$\sqrt{3}$,
∴BE=AB×tan30°=1,AE=2,∠AEB1=∠AEB=60°,
∵四边形ABCD是矩形
∴AD∥BC,
∴∠C1AE=∠AEB=60°,
∴△AEC1为等边三角形,
同理△CC1E也为等边三角形,
∴EC=EC1=AE=2,
∴BC=BE+EC=3,
故选B.
点评 本题考查了翻折变换(折叠问题),矩形的性质,等边三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
14.去年我市有56940名初中毕业生参加升学考试,为了了解这56940名考生的数学成绩.从中抽取2000名考生的数学成绩进行统计分析.在这个问题中样本是( )
| A. | 56940名考生 | B. | 所抽取的2000名考生的数学成绩 | ||
| C. | 56940名考生的数学成绩 | D. | 所抽取的2000名考生 |
11.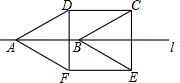 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
 如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )
如图,将边长为2cm的菱形ABCD沿边AB所在的直线l翻折180°得到四边形ABEF,若∠DAB=30°,则四边形CDEF的面积为( )| A. | 2cm2 | B. | 3cm2 | C. | 4cm2 | D. | 6cm2 |
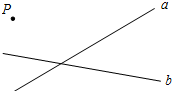 (1)在图中画出表示点P到直线a距离的线段PM;
(1)在图中画出表示点P到直线a距离的线段PM;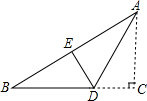 如图,折叠直角三角形纸片的直角,使点C落在AB边上的点E处,已知BC=12,∠B=30°,则DE=4.
如图,折叠直角三角形纸片的直角,使点C落在AB边上的点E处,已知BC=12,∠B=30°,则DE=4.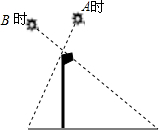 如图,在A时测得旗杆的影长是4米,B时测得的影长是9米,两次的日照光线恰好垂直,则旗杆的高度是6米.
如图,在A时测得旗杆的影长是4米,B时测得的影长是9米,两次的日照光线恰好垂直,则旗杆的高度是6米.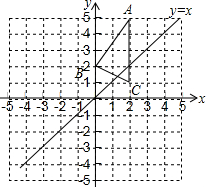 △ABC在平面直角坐标系中的位置如图所示,A、B、C三点的坐标分别为(2,5)、(0,2)、(2,1).
△ABC在平面直角坐标系中的位置如图所示,A、B、C三点的坐标分别为(2,5)、(0,2)、(2,1).