题目内容
13.在一次研究性学习活动中,同学们发现了一种直角三角形的作法,方法是(如图所示):画线段AB,分别以点A、B为圆心,以大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点C,连结AC;再以点C为圆心,以AC长为半径画弧,交AC的延长线于D,连结DB.则△ABD就是直角三角形.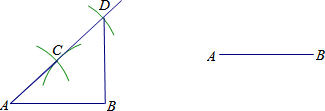
(1)请证明此作法的正确性;
(2)请利用上述方法作一个直角三角形,使其一个锐角为30°(写出作法,保留作图痕迹).
分析 (1)连结BC,如图,利用等腰三角形的性质,由CA=CB得到∠CAB=∠CBA,由CD=CD得到∠D=∠CBD,则∠ABC=∠ABC+∠CBD=$\frac{1}{2}$(∠A+∠CBA+∠CBD+∠D),然后根据三角形内角和得到∠ABD=90°;
(2)由(1)的画法画直角△ABD,只是画出的△ABC为等边三角形,得到∠A=60°,则∠D=30°.
解答 解:(1)连结BC,如图,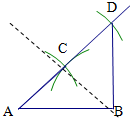
∵CA=CB,
∴∠CAB=∠CBA,
∵CD=CD,
∴∠D=∠CBD,
∴∠ABC=∠ABC+∠CBD=$\frac{1}{2}$(∠A+∠CBA+∠CBD+∠D)=$\frac{1}{2}$×180°=90°,
∴△ABD就是直角三角形;
(2)画线段AB,分别以点A、B为圆心,以AB的长为半径画弧,两弧相交于点C,连结AC;再以点C为圆心,以AC长为半径画弧,交AC的延长线于D,连结DB.则△ABD就是直角三角形.
如图,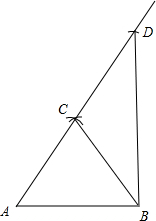
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
18. 如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
 如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )| A. | 6 | B. | 9$\sqrt{2}$ | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
 如图,两个同心圆的半径分别为18cm和30cm,又知∠COD=30°,则阴影部分ABDC的面积为48πcm2.
如图,两个同心圆的半径分别为18cm和30cm,又知∠COD=30°,则阴影部分ABDC的面积为48πcm2. 一块三角形玻璃损坏后,只剩下如图所示的残片,你对图中作哪些数据测量后就可到建材部门割取符合规格的三角形玻璃并说明理由.
一块三角形玻璃损坏后,只剩下如图所示的残片,你对图中作哪些数据测量后就可到建材部门割取符合规格的三角形玻璃并说明理由. 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°. 如图,在等腰梯形ABCD中,AD∥BC,点E、F分别是BD、BC的中点,已知AD=6,BC=12,EF=4,则梯形ABCD的周长为( )
如图,在等腰梯形ABCD中,AD∥BC,点E、F分别是BD、BC的中点,已知AD=6,BC=12,EF=4,则梯形ABCD的周长为( ) 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD,与∠AOB的平分线交于点F,若∠AOB=60°,则OF:FE的值为3:1.
如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD,与∠AOB的平分线交于点F,若∠AOB=60°,则OF:FE的值为3:1. 数学实验课上,同学们调查知道:本乡位于距离学校不远处最高的山顶上的电信发射台铁塔高30米,为了测量此小山相对学校的高度,在学校里操场上用自制的测仰角的仪器做测试实验,如图:在一个地方测的仰角为α=45°,仰角β=60°,求此山的高.
数学实验课上,同学们调查知道:本乡位于距离学校不远处最高的山顶上的电信发射台铁塔高30米,为了测量此小山相对学校的高度,在学校里操场上用自制的测仰角的仪器做测试实验,如图:在一个地方测的仰角为α=45°,仰角β=60°,求此山的高.