题目内容
8. 将一根24cm长的筷子置于底面直径为8cm,内部深度为15cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
将一根24cm长的筷子置于底面直径为8cm,内部深度为15cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )| A. | h≥7cm | B. | h≤16cm | C. | 7cm≤h≤9cm | D. | 7cm≤h≤16cm |
分析 如图,当筷子的底端在A点时,筷子露在杯子外面的长度最短;当筷子的底端在D点时,筷子露在杯子外面的长度最长.然后分别利用已知条件根据勾股定理即可求出h的取值范围.
解答  解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
解:如图,当筷子的底端在D点时,筷子露在杯子外面的长度最长,
∴h=24-15=9cm;
当筷子的底端在A点时,筷子露在杯子外面的长度最短,
在Rt△ABD中,AD=15cm,BD=8cm,
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{1{5}^{2}+{8}^{2}}$=17cm,
∴此时h=24-17=7cm,
所以h的取值范围是7cm≤h≤9cm.
故选C.
点评 本题考查了勾股定理的应用,能够读懂题意和求出h的值最大值与最小值是解题关键.

练习册系列答案
相关题目
19.如图放置的四个几何体中,主视图是圆形的几何体共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.若方程组$\left\{\begin{array}{l}{4x+3y=5}\\{kx+(1-k)y=8}\end{array}\right.$的解中,x的值比y的值的相反数大1,则k的值为( )
| A. | 3 | B. | -3 | C. | 2 | D. | 无答案 |
18. 如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
 如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )| A. | 6 | B. | 9$\sqrt{2}$ | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
 如图,两个同心圆的半径分别为18cm和30cm,又知∠COD=30°,则阴影部分ABDC的面积为48πcm2.
如图,两个同心圆的半径分别为18cm和30cm,又知∠COD=30°,则阴影部分ABDC的面积为48πcm2.
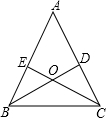 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BE=CD.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BE=CD.