题目内容
9.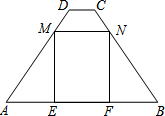 如图,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M、N分别在边AD、BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E、F
如图,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M、N分别在边AD、BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E、F(1)求梯形ABCD的面积;
(2)设AE=x,用含x的代数式表示四边形MEFN的面积;
(3)试判断四边形MEFN能否为正方形?若能,求出正方形MEFN的面积;若不能,请说明理由.
分析 (1)利用等腰梯形的性质结合勾股定理得出梯形的高,进而得出答案;
(2)利用相似三角形的判定与性质表示出ME的长,进而表示四边形MEFN的面积;
(3)利用(2)中所求得出x的值,进而得出正方形MEFN的面积.
解答  解:(1)过点D作DN⊥AB于点N,
解:(1)过点D作DN⊥AB于点N,
∵在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5,
∴AN=$\frac{1}{2}$×(7-1)=3,
∴DN=$\sqrt{A{D}^{2}-A{N}^{2}}$=4,
∴梯形ABCD的面积为:$\frac{1}{2}$×(1+7)×4=16;
(2)∵AE=x,AD=BC,
∴BF=x,则EF=7-2x,
∵ME∥DN,
∴△AEM∽△AND,
∴$\frac{AE}{AN}$=$\frac{ME}{DN}$,
∴$\frac{x}{3}$=$\frac{ME}{4}$,
解得:ME=$\frac{4}{3}$x,
∴用含x的代数式表示四边形MEFN的面积为:(7-2x)•$\frac{4}{3}$x=-$\frac{8}{3}$x2+$\frac{28}{3}$x,
(3)当四边形MEFN为正方形,由(2)得:
则$\frac{4}{3}$x=7-2x,
解得:x=$\frac{21}{10}$,
故正方形MEFN的面积为:$\frac{4}{3}$x2=$\frac{4}{3}$×$\frac{21×21}{100}$=$\frac{147}{25}$.
点评 此题主要考查了相似三角形的判定与性质以及等腰梯形的性质等知识,正确表示出ME的长是解题关键.

练习册系列答案
相关题目
19.如图放置的四个几何体中,主视图是圆形的几何体共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18. 如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
 如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )| A. | 6 | B. | 9$\sqrt{2}$ | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |

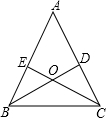 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BE=CD.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BE=CD. 一块三角形玻璃损坏后,只剩下如图所示的残片,你对图中作哪些数据测量后就可到建材部门割取符合规格的三角形玻璃并说明理由.
一块三角形玻璃损坏后,只剩下如图所示的残片,你对图中作哪些数据测量后就可到建材部门割取符合规格的三角形玻璃并说明理由.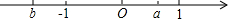 实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.
实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a. 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.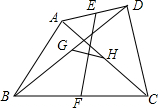 如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足条件AB=CD时,有EF⊥GH.
如图,在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足条件AB=CD时,有EF⊥GH.