题目内容
11.在平面直角坐标系中,已知点E(-6,3)、F(-2,-2),以原点O为位似中心,按比例尺3:1把△EFO缩小,则点E对应点E′的坐标为(-2,1)或(2,-1).分析 根据位似变换的性质计算即可.
解答 解:∵点E的坐标为(-6,3),以原点O为位似中心,按比例尺3:1把△EFO缩小,
∴点E对应点E′的坐标为(-6×$\frac{1}{3}$,3×$\frac{1}{3}$)或(-6×(-$\frac{1}{3}$),3×(-$\frac{1}{3}$)),
即(-2,1)或(2,-1).
故答案为:(-2,1)或(2,-1).
点评 本题考查的是位似变换的性质、坐标与图形的性质,掌握在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,设每次降价的百分率为x,则下面所列的方程中正确的是( )
| A. | 560(1-x)2=315 | B. | 560(1+x)2=315 | C. | 560(1-2x)2=315 | D. | 560(1-x2)=315 |
16. 如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
 如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )
如图,在△ABC中,AD、BE是两条中线,则S△ABP:S△EDP=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
3.若多项式x2+mx+12因式分解的结果是(x-2)(x-6),则m的值是( )
| A. | 8 | B. | -4 | C. | -8 | D. | 4 |
1. 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于A(-3,2),B(2,n),则不等式ax+b<$\frac{k}{x}$的解集为( )| A. | -3<x<2 | B. | -3<x<0或x>2 | C. | x>-3 | D. | x<2 |
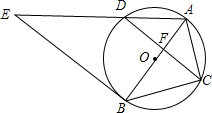 如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.