题目内容
18. 如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )
如图,Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,∠ACD=30°,那么下列结论正确的是( )| A. | AD=$\frac{1}{2}$CD | B. | AC=$\frac{1}{2}$AB | C. | BD=$\frac{1}{2}$BC | D. | CD=$\frac{1}{2}$AB |
分析 根据30°角所对的直角边等于斜边的一半解答即可.
解答 解:∵∠ACB=90°,∠ACD=30°,
∴AD=$\frac{1}{2}$AC,A错误;
∵∠ACD+∠A=90°,∠B+∠A=90°,
∴∠ACD=∠B=30°,
∴AC$\frac{1}{2}$AB,B正确;
CD=$\frac{1}{2}$BC,C、D错误;
故选:B.
点评 本题考查的是直角三角形的性质,掌握30°角所对的直角边等于斜边的一半是解题的关键.

练习册系列答案
相关题目
9.下列线段能构成三角形的是( )
| A. | 2,7,4 | B. | 5,7,12 | C. | 7,15,10 | D. | 4,3,9 |
13.下列说法中正确的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 圆心角是圆周角的2倍 | |
| C. | 三角形的外心到三角形各边的距离相等 | |
| D. | 从圆外一点可以引圆的两条切线,这一点和圆心的连线平分两条切线的夹角 |
3.在平面直角坐标系中,把直线y=-2x+3沿y轴向上平移两个单位长度后,得到的直线的函数关系式为( )
| A. | y=-2x+1 | B. | y=-2x-5 | C. | y=-2x+5 | D. | y=-2x+7 |
20.已知Rt△ABC中,∠C=90°,AC=1,BC=3,则AB的取值范围是( )
| A. | 3.0<AB<3.1 | B. | 3.1<AB<3.2 | C. | 3.2<AB<3.3 | D. | 3.3<AB<3.4 |
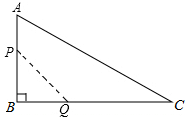 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围) 如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOD+∠COB的度数为180度.
如图,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOD+∠COB的度数为180度. 如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.