题目内容
20. 完成下面的推理过程.
完成下面的推理过程.如图,已知AB∥CD,∠B+∠D=180°,试判断BC与DE之间的位置关系?并证明.
解:BC与DE之间的位置关系是BC∥DE.
证明:∵AB∥CD(已知),
∴∠B=∠C(两直线平行,内错角相等)
∵∠B+∠D=180°(已知),
∴∠C+∠D=180°(等量代换)
∴BC∥DE(同旁内角互补,两直线平行)
分析 先根据平行线的性质,得出∠B=∠C,再根据已知条件∠B+∠D=180°,即可得到∠C+∠D=180°,进而判定BC∥DE.
解答 解:BC与DE之间的位置关系是BC∥DE.
证明:∵AB∥CD(已知),
∴∠B=∠C(两直线平行,内错角相等),
∵∠B+∠D=180°(已知),
∴∠C+∠D=180°(等量代换),
∴BC∥DE(同旁内角互补,两直线平行).
故答案为:BC∥DE,已知,∠B=∠C,两直线平行,内错角相等,已知,∠C+∠D=180°,等量代换,BC∥DE,同旁内角互补,两直线平行.
点评 本题主要考查了平行线的性质与判定的综合应用,解题时注意:两直线平行,内错角相等;同旁内角互补,两直线平行.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
9.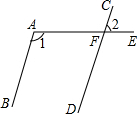 如图,AB∥CD,射线AE交CD于点F,若∠1=105°,则∠2的度数是( )
如图,AB∥CD,射线AE交CD于点F,若∠1=105°,则∠2的度数是( )
 如图,AB∥CD,射线AE交CD于点F,若∠1=105°,则∠2的度数是( )
如图,AB∥CD,射线AE交CD于点F,若∠1=105°,则∠2的度数是( )| A. | 75° | B. | 85° | C. | 95° | D. | 105° |
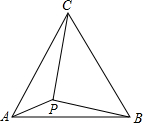 如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为$\frac{2\sqrt{3}}{3}$.
如图,△ABC为等边三角形,AB=2.若P为△ABC内一动点,且满足∠PAB=∠ACP,则线段PB长度的最小值为$\frac{2\sqrt{3}}{3}$.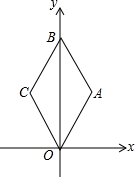 如图,在平面直角坐标系中,菱形OABC的边长为2,点B在y轴上,∠AOC=60°,则点B的坐标为(0,2$\sqrt{3}$).
如图,在平面直角坐标系中,菱形OABC的边长为2,点B在y轴上,∠AOC=60°,则点B的坐标为(0,2$\sqrt{3}$).