题目内容
5.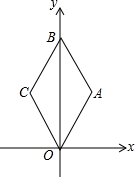 如图,在平面直角坐标系中,菱形OABC的边长为2,点B在y轴上,∠AOC=60°,则点B的坐标为(0,2$\sqrt{3}$).
如图,在平面直角坐标系中,菱形OABC的边长为2,点B在y轴上,∠AOC=60°,则点B的坐标为(0,2$\sqrt{3}$).
分析 连结AC交OB于D,先根据菱形的性质和等边三角形的判定得到△AOC是等边三角形,再根据等边三角形的性质可求OD,进一步求得OB的长,从而得到点B的坐标.
解答  解:连结AC交OB于D,
解:连结AC交OB于D,
∵菱形OABC的边长为2,
∴OC=OA=2,OD=OB,
∵∠AOC=60°,
∴△AOC是等边三角形,
∴OD=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴OB=2OD=2$\sqrt{3}$,
∵点B在y轴上,
∴点B的坐标为(0,2$\sqrt{3}$).
故答案为:(0,2$\sqrt{3}$).
点评 本题考查了坐标与图形性质、菱形的性质、等边三角形的判定与性质等知识,求得OB的长是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列关于正方形的叙述,正确的是( )
| A. | 正方形有且只有一个内切圆 | |
| B. | 正方形有无数个外接圆 | |
| C. | 对角线相等且垂直的四边形是正方形 | |
| D. | 用一根绳子围成一个平面图形,正方形的面积最大 |

 完成下面的推理过程.
完成下面的推理过程.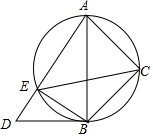 将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.
将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.