题目内容
9.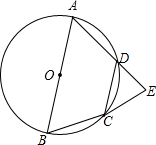 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,BC=CD,CE⊥AD的延长线,垂足为E
如图,四边形ABCD内接于⊙O,AB是⊙O的直径,BC=CD,CE⊥AD的延长线,垂足为E(1)求证:CE是⊙O的切线;
(2)若AB=10,BC=6,求AE的长.
分析 (1)利用圆心角定理的推论得出∠BAC=∠EAC,进而得出∠OCA=∠CAE,利用平行线的性质得出∠E=∠OCE=90°,进而得出CE是⊙O的切线;
(2)利用相似三角形的判定与性质得出$\frac{AB}{AC}$=$\frac{AC}{AE}$,进而得出答案.
解答  (1)证明:连接AC,OC,
(1)证明:连接AC,OC,
∵BC=CD,
∴$\widehat{BC}$=$\widehat{CD}$,
∴∠BAC=∠EAC,
∵AO=CO,
∴∠BAC=∠OCA,
∴∠OCA=∠CAE,
∴CO∥AE,
∴∠E=∠OCE=90°,
∴CE是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠E=90°,
又∵∠BAC=∠EAC,
∴△BAC∽△CAE,
∴$\frac{AB}{AC}$=$\frac{AC}{AE}$,
∵AB=10,BC=6,
∴AC=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴$\frac{10}{8}$=$\frac{8}{AE}$,
解得:AE=6.4.
点评 此题主要考查了切线的判定与性质以及相似三角形的判定与性质等知识,得出△BAC∽△CAE是解题关键.

练习册系列答案
相关题目
4. 如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则tan∠EAB的值是( )
如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则tan∠EAB的值是( )
 如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则tan∠EAB的值是( )
如图,正方形ABCD中,E是BC边上一点,以E为圆心,EC为半径的半圆与以A为圆心,AB为半径的圆弧外切,则tan∠EAB的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |

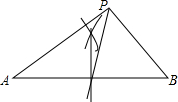 如图,有块直角三角形菜地,分配给张、王、李三家农民耕种,已知张、王、李三家人口分别为2人、4人、6人,菜地按人口比例分配,并要求每户土地均有一部分紧靠水渠AB,P处是三家合用的肥料仓库,所以点P必须是三家地的交界地.
如图,有块直角三角形菜地,分配给张、王、李三家农民耕种,已知张、王、李三家人口分别为2人、4人、6人,菜地按人口比例分配,并要求每户土地均有一部分紧靠水渠AB,P处是三家合用的肥料仓库,所以点P必须是三家地的交界地.