题目内容
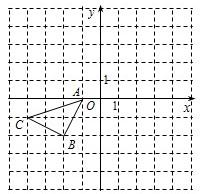 如图所示的正方形网络中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网络中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:(1)分别写出A、B两点的坐标;
(2)作出△ABC关于坐标原点成中心对称的△A1B1C1;
(3)求出△A1B1C1的面积.
考点:作图-旋转变换
专题:
分析:(1)根据图形所示,即可得出A、B两点的坐标;
(2)根据(1),写出C点坐标,再根据关于原点对称的两点横坐标与纵坐标都互为相反数,得出A1、B1、C1的坐标,连接各点,即可得△A1B1C1;
(3)利用△A1B1C1的面积=长方形的面积-三个直角三角形的面积即可求出答案.
(2)根据(1),写出C点坐标,再根据关于原点对称的两点横坐标与纵坐标都互为相反数,得出A1、B1、C1的坐标,连接各点,即可得△A1B1C1;
(3)利用△A1B1C1的面积=长方形的面积-三个直角三角形的面积即可求出答案.
解答: 解:(1)由图形可知,A(-1,0),B(-2,-2);
解:(1)由图形可知,A(-1,0),B(-2,-2);
(2)由图形知C(-4,-1),三点关于原点的中心对称坐标A1(1,0),
B1(2,2),C1(4,1),顺次连接得到△A1B1C1,如图所示:
(3)△A1B1C1的面积
=3×2-
×2×1-
×3×1-
×2×1
=6-1-1.5-1
=2.5.
 解:(1)由图形可知,A(-1,0),B(-2,-2);
解:(1)由图形可知,A(-1,0),B(-2,-2);(2)由图形知C(-4,-1),三点关于原点的中心对称坐标A1(1,0),
B1(2,2),C1(4,1),顺次连接得到△A1B1C1,如图所示:
(3)△A1B1C1的面积
=3×2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=6-1-1.5-1
=2.5.
点评:本题考查了作图-旋转变换,关于坐标原点成中心对称的两图形的对应点的坐标关系:它们的横纵坐标都互为相反数;也考查了坐标的表示以及三角形的面积.

练习册系列答案
相关题目
 如图,大正方形的边长为a,小正方形的边长为b,
如图,大正方形的边长为a,小正方形的边长为b,
