题目内容
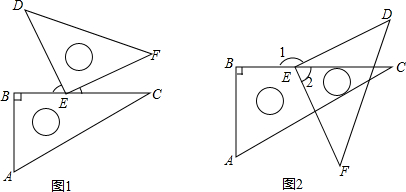
如图①,△ABC中,∠ACB=90°,CD⊥AB于D.
(1)若AD=3,CD=4,则AC= ,如果设BD=x,则BC2可以用含有x的代数式表示为 ,所以,利用△ABC三边的关系可以求得x的值为 ;
(2)若AD=m,BD=n,CD=p,求证:p2=mn;
(3)应用(2)中的结论解决下面的问题:
如图②,点C在x轴上,⊙C交x轴于点A(-2,0)、D,交y轴于点B(0,4),抛物线y=ax2+bx+c经过A、B、D三点,能否在第一象限的该抛物线上找到一点P,使△BDP的面积最大?如果能,请求出此时点P的坐标和△BDP的面积;如果不能,请说明理由.

(1)若AD=3,CD=4,则AC=
(2)若AD=m,BD=n,CD=p,求证:p2=mn;
(3)应用(2)中的结论解决下面的问题:
如图②,点C在x轴上,⊙C交x轴于点A(-2,0)、D,交y轴于点B(0,4),抛物线y=ax2+bx+c经过A、B、D三点,能否在第一象限的该抛物线上找到一点P,使△BDP的面积最大?如果能,请求出此时点P的坐标和△BDP的面积;如果不能,请说明理由.

考点:圆的综合题
专题:综合题
分析:(1)在Rt△ACD中利用勾股定理计算出AC=5,再证明Rt△BCD∽Rt△BAC,于是利用相似比得BC2=BD•BA=x2+3x;然后由勾股定理得BC2=AB2-AC2,所以x2+3x=(3+x)2-52,然后解方程可求出x;
(2)证明Rt△ACD∽Rt△CBD,利用相似比即可得到结论;
(3)连结BD,如图②,根据圆周角定理得∠ABD=90°,则可运用(2)中的结论计算出OD=8,则D点坐标为(8,0),接着利用待定系数法求出直线BD的解析式为y=-
x+4;抛物线解析式为y=-
x2+
x+4,作PH⊥x轴交BD于E点,如图,根据二次函数图象上点的坐标特征可设P点坐标为(t,-
t2+
t+4),则E点坐标为(t,-
t+4),根据三角形面积公式和S△BDP=S△BEP+S△DEP计算得到S△BDP=-t2+8t,然后根据二次函数的最值问题求出使△BDP的面积最大的t的值,从而得到P点坐标和△BDP的面积的最大值.
(2)证明Rt△ACD∽Rt△CBD,利用相似比即可得到结论;
(3)连结BD,如图②,根据圆周角定理得∠ABD=90°,则可运用(2)中的结论计算出OD=8,则D点坐标为(8,0),接着利用待定系数法求出直线BD的解析式为y=-
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
解答:(1)解:在Rt△ACD中,∵AD=3,CD=4,
∴AC=
=5,
∵∠CBD=∠ABC,
∴Rt△BCD∽Rt△BAC,
∴
=
,
∴BC2=BD•BA=x(x+3)=x2+3x;
∵BC2=AB2-AC2,
∴x2+3x=(3+x)2-52,解得x=
;
故答案为5,x2+3x,
;
(2)证明:∵∠ACD+∠DCB=90°,∠A+∠ACD=90°,
∴∠A=∠DCB,
∴Rt△ACD∽Rt△CBD,
∴
=
,即
=
,
∴p2=mn;
(3)解:能.
连结BD,如图②,
∵AD为直径,
∴∠ABD=90°,
由(2)得OB2=OA•OD,即42=2OD,解得OD=8,
∴D点坐标为(8,0),
设直线BD的解析式为y=kx+b,
把B(0,4)、D(8,0)代入得
,解得
,
∴直线BD的解析式为y=-
x+4;
设抛物线的解析式为y=a(x+2)(x-8),
把B(0,4)代入得a×2×(-8)=4,解得a=-
,
∴抛物线解析式为y=-
(x+2)(x-8)=-
x2+
x+4,
作PH⊥x轴交BD于E点,如图,
设P点坐标为(t,-
t2+
t+4),则E点坐标为(t,-
t+4),
∴S△BDP=S△BEP+S△DEP
=
•t•(-
t2+
t+4+
t-4)+
•(8-t)•(-
t2+
t+4+
t-4)
=
•8•(-
t2+2t)
=-t2+8t
=-(t-4)2+16,
∴当t=4时,△BDP的面积最大,此时P点坐标为(4,6),△BDP的面积的最大值为16.
∴AC=
| AD2+CD2 |
∵∠CBD=∠ABC,
∴Rt△BCD∽Rt△BAC,
∴
| BC |
| BA |
| BD |
| BC |
∴BC2=BD•BA=x(x+3)=x2+3x;
∵BC2=AB2-AC2,
∴x2+3x=(3+x)2-52,解得x=
| 16 |
| 3 |
故答案为5,x2+3x,
| 16 |
| 3 |
(2)证明:∵∠ACD+∠DCB=90°,∠A+∠ACD=90°,
∴∠A=∠DCB,
∴Rt△ACD∽Rt△CBD,
∴
| AD |
| CD |
| CD |
| BD |
| m |
| p |
| p |
| n |
∴p2=mn;
(3)解:能.
连结BD,如图②,
∵AD为直径,
∴∠ABD=90°,

由(2)得OB2=OA•OD,即42=2OD,解得OD=8,
∴D点坐标为(8,0),
设直线BD的解析式为y=kx+b,
把B(0,4)、D(8,0)代入得
|
|
∴直线BD的解析式为y=-
| 1 |
| 2 |
设抛物线的解析式为y=a(x+2)(x-8),
把B(0,4)代入得a×2×(-8)=4,解得a=-
| 1 |
| 4 |
∴抛物线解析式为y=-
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
作PH⊥x轴交BD于E点,如图,
设P点坐标为(t,-
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
∴S△BDP=S△BEP+S△DEP
=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 4 |
=-t2+8t
=-(t-4)2+16,
∴当t=4时,△BDP的面积最大,此时P点坐标为(4,6),△BDP的面积的最大值为16.
点评:本题考查了圆的综合题:熟练掌握圆周角定理和二次函数的性质;会利用待定系数法求函数解析式;会灵活应用相似比和勾股定理计算线段的长.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
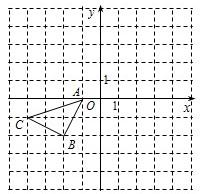 如图所示的正方形网络中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网络中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题: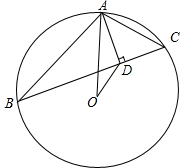 已知⊙O是△ABC的外接圆,AD⊥BC于D,连结AO.
已知⊙O是△ABC的外接圆,AD⊥BC于D,连结AO. 如图,已知线段AB和CD的公共部分为BD,且BD=
如图,已知线段AB和CD的公共部分为BD,且BD=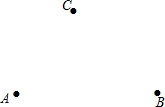 按照下列要求完成作图及相应的问题解答
按照下列要求完成作图及相应的问题解答 黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离;和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)
黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航,渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离;和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)