题目内容
开口向下的抛物线y=mx2-2x+m（m-2）与y轴的交点坐标是（0，3），它与x轴交点的坐标是 ．
考点：抛物线与x轴的交点
专题：
分析：首先求出m的值；当y=0时，得到-x2-2x+3=0；解方程即可解决问题．
解答：解：∵抛物线y=mx2-2x+m（m-2）与y轴的交点坐标是（0，3），
∴m（m-2）=3，解得m=-1或3（不合题意，舍去），
∴当y=0时，-x2-2x+3=0，
解得：x=1或-3，
∴该抛物线与x轴交点的坐标是（1，0）、（-3，0）．
故答案为（1，0）、（-3，0）．
∴m（m-2）=3，解得m=-1或3（不合题意，舍去），
∴当y=0时，-x2-2x+3=0，
解得：x=1或-3，
∴该抛物线与x轴交点的坐标是（1，0）、（-3，0）．
故答案为（1，0）、（-3，0）．
点评：该题主要考查了抛物线与x轴的交点问题；解题的关键是准确求出抛物线解析式，正确运用一元二次方程的知识来求解．
练习册系列答案
相关题目
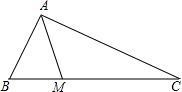在Rt△ABC中，∠BAC=90°，AB=3，M为边长BC上的点，连接AM，如图，如果将△ABM沿直线AM翻折后，点B恰好落在边AC的中点处，那么点M到AC的距离是
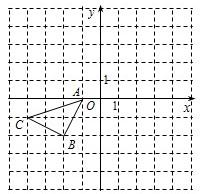如图所示的正方形网络中，△ABC的顶点均在格点上，在所给直角坐标系中解答下列问题：
如图，已知△ABC中，D为AC上一点，E为CB延长线上一点，BE=AD，ED和AB相交于点F，求证：EF：FD=AC：BC．
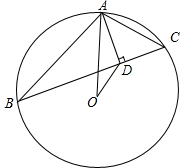已知⊙O是△ABC的外接圆，AD⊥BC于D，连结AO．
如图，已知线段AB和CD的公共部分为BD，且BD=
黄岩岛是我国南沙群岛的一个小岛，渔产丰富．一天某渔船离开港口前往该海域捕鱼．捕捞一段时间后，发现一外国舰艇进入我国水域向黄岩岛驶来，渔船向渔政部门报告，并立即返航，渔政船接到报告后，立即从该港口出发赶往黄岩岛．下图是渔政船及渔船与港口的距离；和渔船离开港口的时间t之间的函数图象．（假设渔船与渔政船沿同一航线航行）