题目内容
5.已知,如图1,直线l与反比例函数y=$\frac{k}{x}$(k>0)位于第一象限的图象相交于A、B两点,并与y轴、x轴分别交于E、F.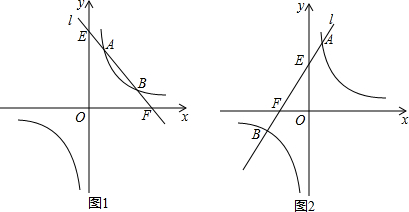
(1)试判断AE与BF的数量关系并说明理由.
(2)如图2,若将直线l绕点A顺时针旋转,使其与反比例函数y=$\frac{k}{x}$的另一支图象相交,设交点为B.试判断AE与BF的数量关系是否依然成立?请说明理由.
分析 (1)作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,由AM∥x轴,得到S△AMN=S△AMO=$\frac{k}{2}$,同理,S△BMN=S△BNO=$\frac{k}{2}$,于是得到S△AMN=S△BMN,推出A、B两点到MN的距离相等,且A、B位于MN同侧,故AB∥MN,得到四边形AMNF与BNME均为平行四边形,根据平行四边形的性质得到AM=FN,EM=BN.根据全等三角形的性质即可得到结论;
(2)作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,由AM∥x轴,得到S△AMN=S△AMO=$\frac{k}{2}$,同理,S△BMN=S△BNO=$\frac{k}{2}$,于是得到S△AMN=S△BMN,推出A、B两点到MN的距离相等,且A、B位于MN同侧,故AB∥MN,得到四边形AMNF与BNME均为平行四边形,根据平行四边形的性质得到AM=FN,EM=BN.根据全等三角形的性质即可得到结论;
解答  解:(1)AE=BF,
解:(1)AE=BF,
理由如下:作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,
∵AM∥x轴,
∴S△AMN=S△AMO=$\frac{k}{2}$,
同理,S△BMN=S△BNO=$\frac{k}{2}$,
∴S△AMN=S△BMN,
即A、B两点到MN的距离相等,且A、B位于MN同侧,故AB∥MN,
∴四边形AMNF与BNME均为平行四边形,
∴AM=FN,EM=BN.
又∵∠AME=∠BNF=90°,
在△EMA与△BNF中,
$\left\{\begin{array}{l}{AM=FN}\\{∠AME=∠BNF}\\{EM=BN}\end{array}\right.$,
∴△EMA≌△BNF,
∴AE=BF;
(2)结论依然成立,AE=BF,
理由: 作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,
作AM⊥y轴于M,BN⊥x轴于N,连接MN、OA、OB、BM、AN,
∵AM∥x轴,
∴S△AMN=S△AMO=$\frac{k}{2}$,
同理,S△BMN=S△BNO=$\frac{k}{2}$,
∴S△AMN=S△BMN,
即A、B两点到MN的距离相等,且A、B位于MN同侧,故AB∥MN,
∴四边形AMNF与BNME均为平行四边形,
∴AM=FN,EM=BN.
又∵∠AME=∠BNF=90°,
在△EMA与△BNF中,
$\left\{\begin{array}{l}{AM=FN}\\{∠AME=∠BNF}\\{EM=BN}\end{array}\right.$,
∴△EMA≌△BNF,
∴AE=BF.
点评 本题考查了反比例函数与一次函数的交点,全等三角形的判定和性质,三角形面积的计算,平行四边形的判定和性质,正确的作出辅助线是解题的关键.

| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | $\sqrt{2}$是2的平方根 | |
| D. | 带根号的数是无理数 |
| A. | 1 | B. | 0 | C. | π | D. | -3 |
| A. | 2016 | B. | -2016 | C. | $\frac{1}{2016}$ | D. | -$\frac{1}{2016}$ |
 如图,等边△ABC内接于⊙O,BC=4,PC切⊙O于C,AP⊥CP,则BP的长为( )
如图,等边△ABC内接于⊙O,BC=4,PC切⊙O于C,AP⊥CP,则BP的长为( )| A. | 5 | B. | 6 | C. | 2$\sqrt{7}$ | D. | 2$\sqrt{6}$ |
