题目内容
14. 如图,等边△ABC内接于⊙O,BC=4,PC切⊙O于C,AP⊥CP,则BP的长为( )
如图,等边△ABC内接于⊙O,BC=4,PC切⊙O于C,AP⊥CP,则BP的长为( )| A. | 5 | B. | 6 | C. | 2$\sqrt{7}$ | D. | 2$\sqrt{6}$ |
分析 首先证明△APB是直角三角形,在RT△APC中求出AP即可解决问题.
解答 解:如图 ,连接OC.
,连接OC.
∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠ACB=60°,
∴$\widehat{AC}$=$\widehat{BC}$,
∴OC⊥AB,
∴∠ACO=∠BCO=30°,
∵PC是切线,
∴OC⊥PC,
∴∠PCO=90°,
∴∠ACP=60°,
∵AP⊥PC,
∴∠APC=90°,∠CAP=30°,
∴∠BAP=∠BAC+∠PAC=90°,
∵PC=$\frac{1}{2}$AC=2,AP2=AC2-PC2=12,
∴PB=$\sqrt{A{B}^{2}+A{P}^{2}}$=$\sqrt{{4}^{2}+12}$=2$\sqrt{7}$.
故选C.
点评 本题考查切线的性质、三角形外接圆的性质、等边三角形的性质、勾股定理等知识,解题的关键是发现△APB是直角三角形,属于中考常考题型.

练习册系列答案
相关题目
4.下面是我国几家银行的标志,其中既是轴对称图形,又是中心对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.2022年冬奥会由北京和张家口两市联合承办.北京到张家口的自驾距离约为196 000米.196 000用科学记数法表示应为( )
| A. | 1.96×105 | B. | 19.6×104 | C. | 1.96×106 | D. | 0.196×106 |
9. 如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )
如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )
 如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )
如图,直线a∥b∥c,直角三角板的直角顶点落在直线b上,若∠1=35°,则∠2等于( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
19.南宁地铁1号线西起西乡塘区石埠,东至南宁火车东站(石埠站-南宁火车东站).总里程约为32100米,这个数据用科学记数法表示可表示为( )
| A. | 321×103米 | B. | 32.1×103米 | C. | 3.21×104米 | D. | 3.21×103米 |
6.下列调查中,适宜采用普查方式的是( )
| A. | 了解一批圆珠笔的寿命 | B. | 了解全国九年级学生身高的现状 | ||
| C. | 检查神舟号载人飞船的各零部件 | D. | 考察人们保护海洋的意识 |
3.若一个多边形的每个内角都等于108°,则这个多边形是( )
| A. | 四边形 | B. | 五边形 | C. | 六边形 | D. | 七边形 |
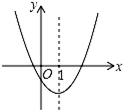 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=1,有下列结论:
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=1,有下列结论: