题目内容
20.某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+500.(1)当销售单价定为35元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,同时又能让消费者获得更多的实惠,那么销售单价应定为多少元?
分析 (1)根据题意列出二次函数关系式,再根据求二次函数最值的方法可解出答案.
(2)把2000元代入上述二次函数关系式,根据函数性质,确定单价.
解答 解:(1)由题意可得:
w=(x-20)•y=(x-20)•(-10x+500)=-10x2+700x-10000=-10(x-35)2+2250,
当销售单价定为35元时,每月可获得最大利润2250元.
故答案为:35.
(2)由题意可知:
-10x2+700x-10000=2000
解这个方程得:x1=30,x2=40.
答:李明想要每月获得2000元的利润,销售单价应定为30元或40元.
点评 本题主要考查了二次函数求最值的方法以及二次函数与一元二次方程的关系.关键是将实际问题转化为求函数最值问题,从而来解决实际问题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
11.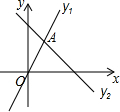 如图,两直线y2=-x+3与y1=2x相交于点A,下列错误的是( )
如图,两直线y2=-x+3与y1=2x相交于点A,下列错误的是( )
 如图,两直线y2=-x+3与y1=2x相交于点A,下列错误的是( )
如图,两直线y2=-x+3与y1=2x相交于点A,下列错误的是( )| A. | x<3时,y1-y2>3 | B. | 当y1>y2时,x>1 | ||
| C. | y1>0且y2>0时,0<x<3 | D. | x<0时,y1<0且y2>3 |
 如图,直线l1∥l2,并且被直线l3,l4所截,则∠α=64°.
如图,直线l1∥l2,并且被直线l3,l4所截,则∠α=64°.

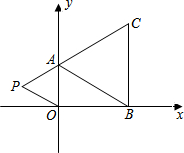 如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,c=2b-a
如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,c=2b-a