题目内容
12.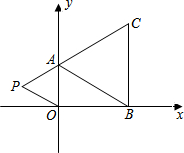 如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,c=2b-a
如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,c=2b-a(1)求a、b、c的值.
(2)如果在第二象限内有一点P(m,0.5),请用含m的式子表示四边形ABOP的面积.
(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)用非负数的性质求解;
(2)把四边形ABOP的面积看成两个三角形面积和,用m来表示;
(3)△ABC可求,是已知量,根据题意,方程即可.
解答 解:(1)由已知|a-2|+(b-3)2=0,
可得:a=2,b=3,c=2b-a=4;
(2)∵S△ABO=$\frac{1}{2}$×2×3=3,S△APO=$\frac{1}{2}$×2×(-m)=-m,
∴S四边形ABOP=S△ABO+S△APO=3+(-m)=3-m;
(3)因为S△ABC=$\frac{1}{2}$×4×3=6,
∵S四边形ABOP=S△ABC
∴3-m=6,
则 m=-3,
所以存在点P(-3,$\frac{1}{2}$)使S四边形ABOP=S△ABC.
点评 本题考查了非负数的性质,三角形及四边形面积的求法,根据题意容易解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.空气的密度是0.001293g/cm3,这个数用科学记数法可表示为( )
| A. | 1.293×10-3 | B. | -1.293×103 | C. | -12.93×10-2 | D. | 0.1293×10-4 |
17.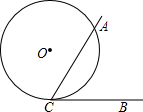 如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
 如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )| A. | $\sqrt{3}$ | B. | $\frac{1}{3}\sqrt{3}$ | C. | π 或$\sqrt{3}$ | D. | $\frac{1}{3}\sqrt{3}$或$\sqrt{3}$ |
1.下列的抛物线中,顶点是(-1,3)的是( )
| A. | y=2(x+1)2+3 | B. | y=-x2+4x+1 | C. | y=2x2+4x-3 | D. | y=-2x2-x+5 |
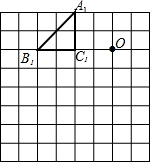 如图,网格图中每一小格的边长都相等.
如图,网格图中每一小格的边长都相等.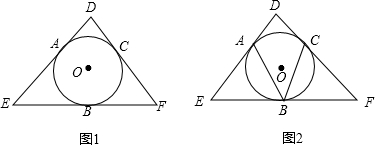
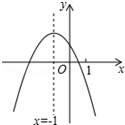 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论: