题目内容
12. 如图,直线l1∥l2,并且被直线l3,l4所截,则∠α=64°.
如图,直线l1∥l2,并且被直线l3,l4所截,则∠α=64°.
分析 首先根据三角形外角的性质,求出∠1的度数是多少;然后根据直线l1∥l2,可得∠α=∠1,据此求出∠α的度数是多少即可.
解答 解:如图1, ,
,
∵∠1+56°=120°,
∴∠1=120°-56°=64°,
又∵直线l1∥l2,
∴∠α=∠1=64°.
故答案为:64°.
点评 此题主要考查了平行线的性质,要熟练掌握,解答此题的关键是要明确:(1)定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.(2)定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.(3)定理3:两条平行线被第三条直线所截,内错角相等. 简单说成:两直线平行,内错角相等.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
2.辐射无处不在,我们一年接受的宇宙射线及其它天然辐线照射量约为3100微西弗(1西弗=1000毫西弗,1毫西弗=1000微西弗),用科学记数法可表示为( )
| A. | 3.1×10-6西弗 | B. | 3.1×106西弗 | C. | 3.1×10-3西弗 | D. | 3.1×103西弗 |
3.空气的密度是0.001293g/cm3,这个数用科学记数法可表示为( )
| A. | 1.293×10-3 | B. | -1.293×103 | C. | -12.93×10-2 | D. | 0.1293×10-4 |
20.下面四个立体图形中,三视图完全相同的是( )
| A. |  | B. |  | C. |  | D. |  |
7.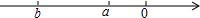 已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )
已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )
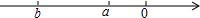 已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )
已知有理数a、b在数轴上表示如图,现比较a、b、-a、-b的大小,正确的是( )| A. | b<a<-a<-b | B. | b<a<-b<-a | C. | -b<a<-a<b | D. | a<b<-b<-a |
17.在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的频率是0.2,则估计盒子中大约有红球( )
| A. | 16个 | B. | 20个 | C. | 25个 | D. | 30个 |
1.下列的抛物线中,顶点是(-1,3)的是( )
| A. | y=2(x+1)2+3 | B. | y=-x2+4x+1 | C. | y=2x2+4x-3 | D. | y=-2x2-x+5 |
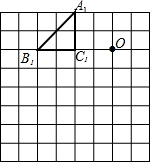 如图,网格图中每一小格的边长都相等.
如图,网格图中每一小格的边长都相等.