题目内容
5．按图中所示的两种方式分割正方形，你能分别得到什么结论？
分析 第一个图形：边长为a+b的大正方形的面积=四个部分的面积之和；
第二个图形：边长为x+y的大正方形的面积=五个部分的面积之和，根据正方形和矩形的面积公式写出多项式即可．
解答 解：第一个图形，（a+b）2=a2+ab+ab+b2=a2+2ab+b2；
第二个图形，（x+y）2=4xy+（x-y）2，
通过列出代数式可以得到：完全平方公式及其变形，两个数的和（或差）的平方，等于这两个数的平方和加上（或减去）这两个数的积的2倍．
点评 本题考查对完全平方公式几何意义的理解，应从整体和部分两方面来理解完全平方公式的几何意义，主要围绕图形面积展开分析．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
如图所示，有一条宽度相等的小路穿过矩形草地ABCD，若AB=60m，BC=81m，AE=100m，则这条小路的面积是多少？
17．在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球（ ）
| A． | 16个 | B． | 20个 | C． | 25个 | D． | 30个 |
13．已知实数x，y，z满足$\left\{\begin{array}{l}{x+y+z=5}\\{4x+y-2z=2}\end{array}\right.$，则代数式4x-4z+1的值是（ ）
| A． | -3 | B． | 3 | C． | -7 | D． | 7 |
10．已知关于x的不等式组$\left\{\begin{array}{l}{x-m≥n}\\{2x-m＜2n+1}\end{array}\right.$的解集为3≤x＜5，则m-n的值是（ ）
| A． | -9 | B． | 9 | C． | 5 | D． | -5 |
17．
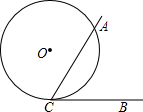如图，∠ACB=60○，半径为1的⊙O切BC于点C，若将⊙O在直线CB上沿某一方向滚动，当滚动到⊙O与CA也相切时，圆心O移动的水平距离为（ ）
如图，∠ACB=60○，半径为1的⊙O切BC于点C，若将⊙O在直线CB上沿某一方向滚动，当滚动到⊙O与CA也相切时，圆心O移动的水平距离为（ ）| A． | $\sqrt{3}$ | B． | $\frac{1}{3}\sqrt{3}$ | C． | π 或$\sqrt{3}$ | D． | $\frac{1}{3}\sqrt{3}$或$\sqrt{3}$ |
14．
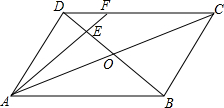如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则S△DEF：S△BAE=（ ）
如图所示，在平行四边形ABCD中，AC与BD相交于点O，E为OD的中点，连接AE并延长交DC于点F，则S△DEF：S△BAE=（ ）| A． | 1：4 | B． | 1：3 | C． | 1：8 | D． | 1：9 |
