题目内容
1．用换元法因式分解：（1）（x2+x+1）（x2+x+2）-12；
（2）（x2-x）（x2-x-14）+24．
分析 （1）将原式展开，是关于x的四次多项式，分解因式较困难．我们不妨将x2+x看作一个整体，并用字母y来替代，于是原题转化为关于y的二次三项式的因式分解问题了．
（2）把（x2-x）看作一个整体，然后利用十字相乘法进行因式分解．
解答 解：（1）设x2+x=y，则
原式=（y+1）（y+2）-12=y2+3y-10
=（y-2）（y+5）=（x2+x-2）（x2+x+5）
=（x-1）（x+2）（x2+x+5）．
（2）原式=（x2-x-3）（x2-x-8）=（x-2）（x+1）（x-4）（x+3）．
点评 本题考查了因式分解-十字相乘法．对于展开后次数较高的因式分解，不要急于展开，要多观察查找规律．常用换元法来解决．
练习册系列答案
阶梯计算系列答案
相关题目
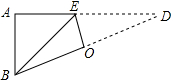如图，直角△ABD中，∠A=90°，AB=3cm，AD=9cm，将此三角形折叠，使点B与点D重合，折痕为EO，则△EOD的面积为$\frac{15}{4}$cm2．
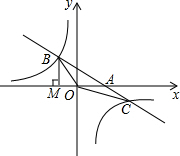如图，已知直线y=-x-（k+1）与双曲线y=$\frac{k}{x}$相交于B、C两点，与x轴相交于A点，BM⊥x轴交x轴于点M，S△OMB=$\frac{3}{2}$
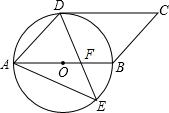如图，四边形ABCD是平行四边形，以AB为直径的圆O经过点D，E是⊙O上一点，且∠AED=45°，DE交直径AB于点F．