题目内容
11.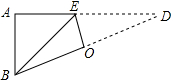 如图,直角△ABD中,∠A=90°,AB=3cm,AD=9cm,将此三角形折叠,使点B与点D重合,折痕为EO,则△EOD的面积为$\frac{15}{4}$cm2.
如图,直角△ABD中,∠A=90°,AB=3cm,AD=9cm,将此三角形折叠,使点B与点D重合,折痕为EO,则△EOD的面积为$\frac{15}{4}$cm2.
分析 设ED=xcm,则AE=(9-x)cm,由翻折的性质可知:S△EBO=S△EDO,BE=ED=x,在Rt△AEB中,由勾股定理可求得DE=5,然后根据S△EOD=$\frac{1}{2}({S}_{△ABD}-{S}_{△ABE})$求解即可.
解答 解:设ED=xcm,则AE=(9-x)cm,由翻折的性质可知:BE=ED=x.
在Rt△AEB中,由勾股定理可知:BE2=AE2+AB2,即x2=(9-x)2+32,
解得:x=5.
∴ED=5cm.
由翻折的性质可知:S△EBO=S△EDO.
∵S△EBO=S△EDO,
∴S△EOD=$\frac{1}{2}({S}_{△ABD}-{S}_{△ABE})$=$\frac{1}{2}×(\frac{1}{2}×3×9-\frac{1}{2}×3×4)$=$\frac{15}{4}$.
故答案为:$\frac{15}{4}$.
点评 本题主要考查的是翻折的性质,利用翻折的性质、勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
1. 如图,在△ABC中,点O为重心,则S△DOE:S△BOC=( )
如图,在△ABC中,点O为重心,则S△DOE:S△BOC=( )
 如图,在△ABC中,点O为重心,则S△DOE:S△BOC=( )
如图,在△ABC中,点O为重心,则S△DOE:S△BOC=( )| A. | 1:4 | B. | 1:3 | C. | 1:2 | D. | 2:3 |
19.若⊙O的半径为5,OP=5,则点P与⊙O的位置关系是( )
| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 点P在⊙O上或⊙O外 |
16.下列图形中,正方体的表面展开图是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,AC∥BD,AD、BC相交于E,EF∥BD,求证:$\frac{1}{AC}$+$\frac{1}{BD}$=$\frac{1}{EF}$.
如图,AC∥BD,AD、BC相交于E,EF∥BD,求证:$\frac{1}{AC}$+$\frac{1}{BD}$=$\frac{1}{EF}$.