题目内容
定义：我们把对角线互相垂直的四边形叫做和美四边形，对角线交点称为和美四边形的中心．如图四边形ABCD是和美四边形，若AB=3，BC=2，CD=4，求AD的长．考点：勾股定理
专题：新定义
分析：在Rt△AOB、Rt△DOC中分别表示出AO2、DO2，从而在Rt△ADO中利用勾股定理即可得出AD的长度．
解答：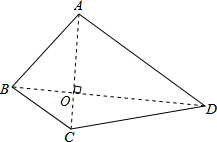
解：如图，连接AC、BD交于点O，则AC⊥BD．
∵在Rt△AOB中，AO2=AB2-BO2，Rt△DOC中，DO2=DC2-CO2，AB=3，BC=2，CD=4，
∴可得AD2=AO2+DO2=AB2-BO2+DC2-CO2=AB2+DC2-BC2=32+42-22=21，
即可得AD=
．
解：如图，连接AC、BD交于点O，则AC⊥BD．∵在Rt△AOB中，AO2=AB2-BO2，Rt△DOC中，DO2=DC2-CO2，AB=3，BC=2，CD=4，
∴可得AD2=AO2+DO2=AB2-BO2+DC2-CO2=AB2+DC2-BC2=32+42-22=21，
即可得AD=
| 21 |
点评：此题考查了勾股定理的知识，解答本题的关键是在Rt△AOB、Rt△DOC中分别表示出AO2、DO2，需要我们熟练掌握勾股定理的表达形式．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
如图，在△ABC中，点D在BC 上，点E 在AC 上，AD交BE于F．已知EG∥AD交BC于G，EH⊥BE交BC于H，∠HEG=50°．
如图，P是正方形ABCD对角线BD上一点，PE⊥DC，PF⊥BC，垂足分别为点E、F．请判断AP与EF的数量关系，并证明你的判断．