题目内容
 如图,在△ABC中,点D在BC 上,点E 在AC 上,AD交BE于F.已知EG∥AD交BC于G,EH⊥BE交BC于H,∠HEG=50°.
如图,在△ABC中,点D在BC 上,点E 在AC 上,AD交BE于F.已知EG∥AD交BC于G,EH⊥BE交BC于H,∠HEG=50°.(1)求∠BFD的度数.
(2)若∠BAD=∠EBC,∠C=42°,求∠BAC的度数.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据垂直的定义可得∠BEH=90°,然后求出∠BEG=40°,再根据两直线平行线,同位角相等可得∠BFD=∠BEG;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BFD=∠EBC+∠ABE=∠ABC,然后根据三角形的内角和定理列式计算即可得解.
(2)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BFD=∠EBC+∠ABE=∠ABC,然后根据三角形的内角和定理列式计算即可得解.
解答:解:(1)∵EH⊥BE,
∴∠BEH=90°,
∵∠HEG=50°,
∴∠BEG=40°,
又∵EG∥AD,
∴∠BFD=∠BEG=40°;
(2)∵∠BFD=∠BAD+∠ABE,∠BAD=∠EBC,
∴∠BFD=∠EBC+∠ABE=∠ABC=40°,
∵∠C=42°,
∴∠BAC=180°-∠ABC-∠C=180°-40°-42°=98°.
∴∠BEH=90°,
∵∠HEG=50°,
∴∠BEG=40°,
又∵EG∥AD,
∴∠BFD=∠BEG=40°;
(2)∵∠BFD=∠BAD+∠ABE,∠BAD=∠EBC,
∴∠BFD=∠EBC+∠ABE=∠ABC=40°,
∵∠C=42°,
∴∠BAC=180°-∠ABC-∠C=180°-40°-42°=98°.
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,平行线的性质,熟记各性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,点阵中以相邻4个点为顶点的小正方形面积为1.
如图,点阵中以相邻4个点为顶点的小正方形面积为1. 如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于E.求阴影部分的面积(结果保留π).
如图,正方形ABCD边长为4,以BC为直径的半圆O交对角线BD于E.求阴影部分的面积(结果保留π).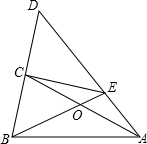 已知:如图,在△ABC中,AB=AC,延长BC到D,使BD=2BC,连接AD,过C作CE⊥BD交AD于点E,连接BE交AC于点O.
已知:如图,在△ABC中,AB=AC,延长BC到D,使BD=2BC,连接AD,过C作CE⊥BD交AD于点E,连接BE交AC于点O. 如图,考古学家在一次考古中发现一块破损的圆壁,请你将它复原.
如图,考古学家在一次考古中发现一块破损的圆壁,请你将它复原. 定义:我们把对角线互相垂直的四边形叫做和美四边形,对角线交点称为和美四边形的中心.如图四边形ABCD是和美四边形,若AB=3,BC=2,CD=4,求AD的长.
定义:我们把对角线互相垂直的四边形叫做和美四边形,对角线交点称为和美四边形的中心.如图四边形ABCD是和美四边形,若AB=3,BC=2,CD=4,求AD的长. 某校初中三个年级学生总人数为3000人,三个年级学生人数所占比例如图,则七年级学生人数为
某校初中三个年级学生总人数为3000人,三个年级学生人数所占比例如图,则七年级学生人数为