题目内容
1.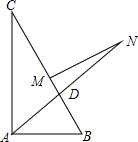 在直角△ABC中,∠A为直角,AB=6,AC=8,AD是∠A的角平分线,MN是边BC的垂直平分线,则MN的长为( )
在直角△ABC中,∠A为直角,AB=6,AC=8,AD是∠A的角平分线,MN是边BC的垂直平分线,则MN的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 10 |
分析 作NE⊥AB于E,NF⊥AC于F,连接NC,NB,根据角平分线的性质得到NF=NE,根据线段的垂直平分线的性质得到NC=NB,证明Rt△NFC≌Rt△NEB,得到CF=BE,求出BE的长,根据勾股定理计算即可.
解答 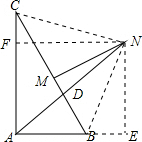 解:作NE⊥AB于E,NF⊥AC于F,连接NC,NB,
解:作NE⊥AB于E,NF⊥AC于F,连接NC,NB,
∵AD是∠A的角平分线,
∴NE=NF,
∵MN是边BC的垂直平分线,
∴NC=NB,
在Rt△NFC和Rt△NEB中,
$\left\{\begin{array}{l}{NC=NB}\\{NF=NE}\end{array}\right.$,
∴Rt△NFC≌Rt△NEB,
∴CF=BE,
∵6+BE=8-CF,
∴CF=BE=1,∴NE=AF=7,
由勾股定理得,NB=$\sqrt{B{E}^{2}+N{E}^{2}}$=5$\sqrt{2}$,
∵∠A为直角,AB=6,AC=8,
∴BC=10,则NB=5,
∴MN=5,
故选:C.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
12.Rt△ABC中,∠ACB=90°,若∠ACD=50°,则与∠BCD相邻的外角度数是( )
| A. | 130° | B. | 140° | C. | 30° | D. | 40° |
11.下列计算中错误的是( )
| A. | (-20)-(-5)=-15 | B. | 1-(+7)=-6 | C. | 0-(+2)=-2 | D. | (-5)-(+5)=0 |
 由四个边长分别为a,b,c的直角三角形拼成一个新的图形.试用两种不同的方法计算这个图形的面积,并说说你发现了什么.
由四个边长分别为a,b,c的直角三角形拼成一个新的图形.试用两种不同的方法计算这个图形的面积,并说说你发现了什么. 已知:如图,AD=CB,AB=DC,BE⊥AC,垂足为E,DF⊥AC,垂足为F.
已知:如图,AD=CB,AB=DC,BE⊥AC,垂足为E,DF⊥AC,垂足为F.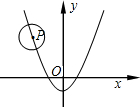 如图,已知⊙P的半径为2,圆心P在抛物线y=$\frac{1}{2}$x2-3上运动,当⊙P与x轴相切时,圆心P的坐标为(-$\sqrt{10}$,2)或($\sqrt{10}$,2)或(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2).
如图,已知⊙P的半径为2,圆心P在抛物线y=$\frac{1}{2}$x2-3上运动,当⊙P与x轴相切时,圆心P的坐标为(-$\sqrt{10}$,2)或($\sqrt{10}$,2)或(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2).