题目内容
13.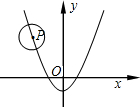 如图,已知⊙P的半径为2,圆心P在抛物线y=$\frac{1}{2}$x2-3上运动,当⊙P与x轴相切时,圆心P的坐标为(-$\sqrt{10}$,2)或($\sqrt{10}$,2)或(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2).
如图,已知⊙P的半径为2,圆心P在抛物线y=$\frac{1}{2}$x2-3上运动,当⊙P与x轴相切时,圆心P的坐标为(-$\sqrt{10}$,2)或($\sqrt{10}$,2)或(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2).
分析 根据切线的性质得点P到x轴的距离为2,即P点的纵坐标为2或-2,然后根据二次函数图象上点的坐标特征,分别计算出y=2或y=-2所对应的自变量的值,从而可确定P点坐标.
解答 解:∵⊙P与x轴相切,
∴点P到x轴的距离为2,
即P点的纵坐标为2或-2,
当y=2时,$\frac{1}{2}$x2-3=2,解得x1=-$\sqrt{10}$,x2=$\sqrt{10}$,则P点坐标为(-$\sqrt{10}$,2)或($\sqrt{10}$,2);
当y=-2时,$\frac{1}{2}$x2-3=-2,解得x1=-$\sqrt{2}$,x2=$\sqrt{2}$,则P点坐标为(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2),
综上所述,圆心P的坐标为(-$\sqrt{10}$,2)或($\sqrt{10}$,2)或(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2).
故答案为(-$\sqrt{10}$,2)或($\sqrt{10}$,2)或(-$\sqrt{2}$,-2)或($\sqrt{2}$,-2).
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了二次函数图象上点的坐标特征.注意分类讨论思想的运用.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
5. y=ax2+bx+1的大致图象如图所示,那么函数y=ax+b的图象不经过( )
y=ax2+bx+1的大致图象如图所示,那么函数y=ax+b的图象不经过( )
 y=ax2+bx+1的大致图象如图所示,那么函数y=ax+b的图象不经过( )
y=ax2+bx+1的大致图象如图所示,那么函数y=ax+b的图象不经过( )| A. | 一象限 | B. | 二象限 | C. | 三象限 | D. | 四象限 |
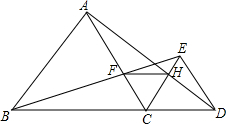 如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,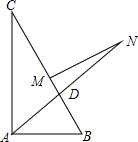 在直角△ABC中,∠A为直角,AB=6,AC=8,AD是∠A的角平分线,MN是边BC的垂直平分线,则MN的长为( )
在直角△ABC中,∠A为直角,AB=6,AC=8,AD是∠A的角平分线,MN是边BC的垂直平分线,则MN的长为( )
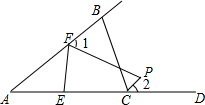 如图,△ABC中,点D在AC的延长线上,E、F分别在边AC和AB上,∠BFE和∠BCD的平分线相交于点P,若∠B=80°,∠FEC=70°,则∠1-∠2=15°°;∠P=95°°.
如图,△ABC中,点D在AC的延长线上,E、F分别在边AC和AB上,∠BFE和∠BCD的平分线相交于点P,若∠B=80°,∠FEC=70°,则∠1-∠2=15°°;∠P=95°°.