题目内容
6.计算:(1)$\sqrt{{3}^{2}}$=3. $\sqrt{{0}^{2}}$=0. $\sqrt{(\frac{1}{5})^{2}}$=$\frac{1}{5}$. $\sqrt{(-2)^{2}}$=2.
$\sqrt{(-5)^{2}}$=5.
(2)思考:通过上述计算,可以发现什么规律?并运用发现的规律计算:
①$\sqrt{(3-π)^{2}}$;
②$\sqrt{(a-1)^{2}}(a<1)$;
③$\sqrt{(2-x)^{2}}$.
分析 根据$\sqrt{{a}^{2}}$=|a|进行化简,然后根据绝对值的性质进行化简即可.
解答 解:(1)$\sqrt{{3}^{2}}$=|3|=3; $\sqrt{{0}^{2}}$=|0|=0; $\sqrt{(\frac{1}{5})^{2}}$=|$\frac{1}{5}$|=$\frac{1}{5}$; $\sqrt{(-2)^{2}}$=|-2|=2;$\sqrt{(-5)^{2}}$=|-5|=5.
故答案为:3;0;$\frac{1}{5}$;2;5.
(2)①$\sqrt{(3-π)^{2}}$=|3-π|=π-3;②$\sqrt{(a-1)^{2}}$=|a-1|=1-a;③$\sqrt{(2-x)^{2}}$=|2-x|=$\left\{\begin{array}{l}{2-x(x≤2)}\\{x-2(x>2)}\end{array}\right.$.
点评 本题主要考查的是二次根式的化简,掌握二次根式的性质是解题的关键.

练习册系列答案
相关题目
 如图,已知线段a,c(a<c),画一个Rt△ABC,使∠C=90°,一直角边CB=a,斜边AB=c.
如图,已知线段a,c(a<c),画一个Rt△ABC,使∠C=90°,一直角边CB=a,斜边AB=c.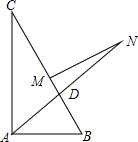 在直角△ABC中,∠A为直角,AB=6,AC=8,AD是∠A的角平分线,MN是边BC的垂直平分线,则MN的长为( )
在直角△ABC中,∠A为直角,AB=6,AC=8,AD是∠A的角平分线,MN是边BC的垂直平分线,则MN的长为( )
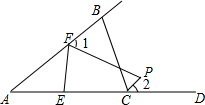 如图,△ABC中,点D在AC的延长线上,E、F分别在边AC和AB上,∠BFE和∠BCD的平分线相交于点P,若∠B=80°,∠FEC=70°,则∠1-∠2=15°°;∠P=95°°.
如图,△ABC中,点D在AC的延长线上,E、F分别在边AC和AB上,∠BFE和∠BCD的平分线相交于点P,若∠B=80°,∠FEC=70°,则∠1-∠2=15°°;∠P=95°°.