题目内容
16. 已知:如图,AD=CB,AB=DC,BE⊥AC,垂足为E,DF⊥AC,垂足为F.
已知:如图,AD=CB,AB=DC,BE⊥AC,垂足为E,DF⊥AC,垂足为F.求证:(1)△ABC≌△CDA;(2)BE=DF.
分析 (1)根据全等三角形的边边边判定定理证明即可;
(2)根据三角形面积公式计算即可.
解答 证明:(1)在△ABC和△CDA中,
$\left\{\begin{array}{l}{AD=CB}\\{CD=AB}\\{AC=CA}\end{array}\right.$,
△ABC≌△CDA.
(2)∵△ABC≌△CDA,
∴S△ABC=S△CDA,
∵S△ABC=$\frac{1}{2}$AC×BE,S△CDA=$\frac{1}{2}$AC×DF,
∴BE=DF.
点评 本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.以下结论,其中正确结论的个数是( )
①整数和分数统称为有理数;
②相反数等于本身的数只有零;
③倒数等于本身的数只有1;
④绝对值等于本身的数只有正数;
⑤最大的负整数是-1;
⑥在有理数中绝对值最小的数是零;
⑦-M的相反数是M;
⑧零减去一个数仍得这个数.
①整数和分数统称为有理数;
②相反数等于本身的数只有零;
③倒数等于本身的数只有1;
④绝对值等于本身的数只有正数;
⑤最大的负整数是-1;
⑥在有理数中绝对值最小的数是零;
⑦-M的相反数是M;
⑧零减去一个数仍得这个数.
| A. | 1个 | B. | 3个 | C. | 5个 | D. | 多于6个 |
5. y=ax2+bx+1的大致图象如图所示,那么函数y=ax+b的图象不经过( )
y=ax2+bx+1的大致图象如图所示,那么函数y=ax+b的图象不经过( )
 y=ax2+bx+1的大致图象如图所示,那么函数y=ax+b的图象不经过( )
y=ax2+bx+1的大致图象如图所示,那么函数y=ax+b的图象不经过( )| A. | 一象限 | B. | 二象限 | C. | 三象限 | D. | 四象限 |
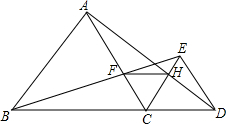 如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,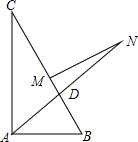 在直角△ABC中,∠A为直角,AB=6,AC=8,AD是∠A的角平分线,MN是边BC的垂直平分线,则MN的长为( )
在直角△ABC中,∠A为直角,AB=6,AC=8,AD是∠A的角平分线,MN是边BC的垂直平分线,则MN的长为( )