题目内容
已知二次函数y=x2+(2m-1)x+m2+2有最小值2.
(1)求m的值;
(2)求该二次函数的顶点坐标和对称轴.
(1)求m的值;
(2)求该二次函数的顶点坐标和对称轴.
考点:二次函数的最值,二次函数的性质
专题:
分析:(1)根据二次函数y=ax2+bx+c的最值为y=
列出关于m的方程,解方程即可;
(2)根据二次函数y=ax2+bx+c的顶点坐标是(-
,
),对称轴直线x=-
,代入数值即可求解.
| 4ac-b2 |
| 4a |
(2)根据二次函数y=ax2+bx+c的顶点坐标是(-
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
解答:解:(1)根据题意得
=2,
解得m=
;
(2)当m=
时,y=x2-
x+
,
对称轴直线x=-
=
,
顶点坐标是(
,2).
| 4(m2+2)-(2m-1)2 |
| 4 |
解得m=
| 1 |
| 4 |
(2)当m=
| 1 |
| 4 |
| 1 |
| 2 |
| 33 |
| 16 |
对称轴直线x=-
-
| ||
| 2 |
| 1 |
| 4 |
顶点坐标是(
| 1 |
| 4 |
点评:本题考查了二次函数的最值,二次函数的性质,求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
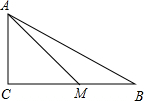 已知在△ABC中,∠C=90°,M在BC上,若AB=17,AM=10,BM=9,求AC、MC的长.
已知在△ABC中,∠C=90°,M在BC上,若AB=17,AM=10,BM=9,求AC、MC的长. 如图所示,∠1=∠2,∠3=∠4,AC、BD相交于点E,求证:AC是线段BD的垂直平分线.
如图所示,∠1=∠2,∠3=∠4,AC、BD相交于点E,求证:AC是线段BD的垂直平分线.