题目内容
已知代数式-3a2-6a+7，用配方法说明，当a取何值时，这个代数式的值最大，最大的值是多少？
考点：配方法的应用
专题：计算题
分析：先利用配方法得到3a2-6a+7=-3（a+1）2+10，再根据非负数的性质得-3（a+1）2+10≤10，由此得到当a=-1时，代数式有最大值10．
解答：解：-3a2-6a+7=-3（a2+2a）+7
=-3（a+1）2+10，
∵3（a+1）2≥0，
∴-3（a+1）2≤0，
∴-3（a+1）2+10≤10，
∴当a取-1时，这个代数式的值最大，最大的值是10．
=-3（a+1）2+10，
∵3（a+1）2≥0，
∴-3（a+1）2≤0，
∴-3（a+1）2+10≤10，
∴当a取-1时，这个代数式的值最大，最大的值是10．
点评：本题考查了配方法的应用：用配方法解一元二次方程，配方法的理论依据是公式a2±2ab+b2=（a±b）2；利用配方法求二次三项式是一个完全平方式时所含字母系数的值．
练习册系列答案
相关题目
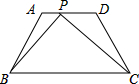如图，在梯形ABCD中，AD∥BC，AB=CD=2，AD=5，在AD边上是否存在一点P，使得△ABP与△DPC相似？若存在，求出线段AP的长；若不存在，请说明理由．
如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．求证：E是BF的中点．