题目内容
2. 如图,长方形ABCD中,边AD长为18,在BC边上取一点E,使BE=5,现沿AE对折,点B恰好落在对角线AC上的F点处.
如图,长方形ABCD中,边AD长为18,在BC边上取一点E,使BE=5,现沿AE对折,点B恰好落在对角线AC上的F点处.(1)求长方形ABCD的面积;
(2)求△ACE中边AE上的高.
分析 (1)根据题意和勾股定理求出FC的长,设AB=x,根据勾股定理列出方程,解方程求出x的值,根据三角形面积公式计算即可;
(2)证明△ABE∽△CHE,根据相似三角形对应边的比相等列出比例式,计算即可.
解答 解:(1)由题意得,BA=AF,BE=EF,
∵AD=18,BE=5,
∴EC=13,又EF=BE=5,
∴FC=$\sqrt{E{C}^{2}-E{F}^{2}}$=12,
设AB=x,则AF=x,
∴x2+182=(x+12)2,
解得,x=7.5,则AB=7.5,
∴长方形ABCD的面积=7.5×18=135;
(2)∵AB=$\frac{15}{2}$,BE=5,
∴AE=$\frac{5\sqrt{13}}{2}$,
作CH⊥AE交AE的延长线于H,
又∵∠B=90°,
∴△ABE∽△CHE,
∴$\frac{AB}{CH}$=$\frac{AE}{EC}$,即$\frac{\frac{15}{2}}{CH}$=$\frac{\frac{5\sqrt{13}}{2}}{13}$,
解得CH=3$\sqrt{13}$,
答:△ACE中边AE上的高为3$\sqrt{13}$.
点评 本题考查的是翻折变换的性质、相似三角形的判定和性质,掌握折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
相关题目
10.下列说法中,一定正确的是( )
| A. | 有一个锐角相等的两个等腰三角形相似 | |
| B. | 底角为45°的两个等腰梯形相似 | |
| C. | 任意两个菱形相似 | |
| D. | 两个等腰直角三角形必相似 |
14. 如图,∠AOB的平分线上一点P到OA的距离为10,Q是OB上任一点,则( )
如图,∠AOB的平分线上一点P到OA的距离为10,Q是OB上任一点,则( )
 如图,∠AOB的平分线上一点P到OA的距离为10,Q是OB上任一点,则( )
如图,∠AOB的平分线上一点P到OA的距离为10,Q是OB上任一点,则( )| A. | PQ>10 | B. | PQ≥10 | C. | PQ<10 | D. | PQ≤10 |
11.下列各式中,y是x的二次函数的是( )
| A. | y=x2-(x-2)2 | B. | x2+y-2=0 | C. | y=ax2+bx+c | D. | y=x2+3x-$\frac{1}{x}$ |
 如图,△ABD≌△ACE,点B和点C是对应顶点,AB=9cm,BD=7cm,AD=4cm,则DC=5cm.
如图,△ABD≌△ACE,点B和点C是对应顶点,AB=9cm,BD=7cm,AD=4cm,则DC=5cm.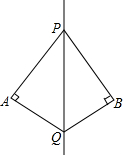 如图,PQ是∠APB的平分线,QA⊥PA于点A,QB⊥PB于点B,试判断点A,B是否关于PQ成轴对称,并说明理由.
如图,PQ是∠APB的平分线,QA⊥PA于点A,QB⊥PB于点B,试判断点A,B是否关于PQ成轴对称,并说明理由.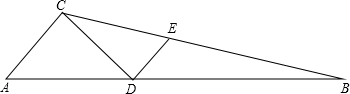 如图,在ABC中,已知D为AB边上一点,AC⊥CD,DE⊥CD,CD:CE=4:5,S△ACD:S△CDB=2:3,则tanA=$\frac{4}{5}$.
如图,在ABC中,已知D为AB边上一点,AC⊥CD,DE⊥CD,CD:CE=4:5,S△ACD:S△CDB=2:3,则tanA=$\frac{4}{5}$. 如图,已知AB=AC,DB=DC,F是AD延长线上的任意一点,△ABF与△ACF全等吗?为什么?
如图,已知AB=AC,DB=DC,F是AD延长线上的任意一点,△ABF与△ACF全等吗?为什么?