题目内容
13.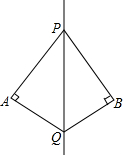 如图,PQ是∠APB的平分线,QA⊥PA于点A,QB⊥PB于点B,试判断点A,B是否关于PQ成轴对称,并说明理由.
如图,PQ是∠APB的平分线,QA⊥PA于点A,QB⊥PB于点B,试判断点A,B是否关于PQ成轴对称,并说明理由.
分析 首先证明△PAQ≌△PBQ,得出PB=PA,QA=QB,进一步利用轴对称图形的性质得出A,B是否关于PQ成轴对称.
解答 解:∵PQ是∠APB的平分线,
∴∠APQ=∠BPQ,
∵QA⊥PA,QB⊥PB,
∴∠A=∠B=90°,
在△PAQ和△PBQ中,
$\left\{\begin{array}{l}{∠A=∠B}\\{∠APQ=∠BPQ}\\{PQ=PQ}\end{array}\right.$,
∴△PAQ≌△PBQ,
∴PB=PA,QA=QB,
∴连接AB,则PQ垂直平分AB,
∴A,B关于PQ成轴对称.
点评 此题考查轴对称图形的性质,掌握轴对称图形的性质对应点的连线被对称轴垂直平分是解决问题的关键.

练习册系列答案
相关题目
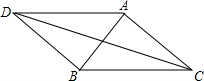 等腰Rt△ABC中,AB=AC,∠BAC=90°,点D在△ABC外,且∠ADB=45°,BD=3,AD=4,求线段DC的长.
等腰Rt△ABC中,AB=AC,∠BAC=90°,点D在△ABC外,且∠ADB=45°,BD=3,AD=4,求线段DC的长.
 △ABC的边BC在直线l上,点D,E是直线l上的两点,且BA=BD,CA=CE
△ABC的边BC在直线l上,点D,E是直线l上的两点,且BA=BD,CA=CE 如图,长方形ABCD中,边AD长为18,在BC边上取一点E,使BE=5,现沿AE对折,点B恰好落在对角线AC上的F点处.
如图,长方形ABCD中,边AD长为18,在BC边上取一点E,使BE=5,现沿AE对折,点B恰好落在对角线AC上的F点处.