题目内容
17. 已知,如图,⊙O的半径为6,弧$\widehat{AC}$的度数为120°,点B为弧$\widehat{AC}$的中点,点D为⊙O上异于A、B、C的三点,OE⊥AD于E,OF⊥CD于F,连接EF.
已知,如图,⊙O的半径为6,弧$\widehat{AC}$的度数为120°,点B为弧$\widehat{AC}$的中点,点D为⊙O上异于A、B、C的三点,OE⊥AD于E,OF⊥CD于F,连接EF.(1)求证:四边形OABC是菱形;
(2)求线段EF的长.
分析 (1)连接OB,根据已知条件得到∠AOB=∠COB=60°,推出△AOB与△COB是等边三角形,根据等边三角形的性质得到OA=OB=BC=OC,于是得到四边形OABC是菱形;
(2)连接AC,交OB于G,由四边形OABC是菱形,得到∠OAC=30°,求得AG=$\frac{\sqrt{3}}{2}$AO=3$\sqrt{3}$,得到AC=2AG=6$\sqrt{3}$,根据三角形的中位线的性质即可得到结论.
解答 解:(1)连接OB,
∵$\widehat{AC}$的度数为120°,点B为弧$\widehat{AC}$的中点,
∴∠AOB=∠COB=60°,
∵AO=BO=CO,
∴△AOB与△COB是等边三角形,
∴OA=OB=BC=OC,
∴四边形OABC是菱形;
(2)连接AC,交OB于G,
∵四边形OABC是菱形,
∴∠OAC=30°,
AC⊥OB,
∴AG=$\frac{\sqrt{3}}{2}$AO=3$\sqrt{3}$,
∴AC=2AG=6$\sqrt{3}$,
∵OE⊥AD于E,OF⊥CD于F,
∴DE=AE.DF=CF,
∴EF=$\frac{1}{2}$AC=3$\sqrt{3}$.
点评 本题考查了圆周角定理,菱形的判定和性质,三角形的中位线的性质,垂径定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
5.下列数据中最小的是( )
| A. | 11011001(二进制数) | B. | 75(十进制数) | ||
| C. | 72(八进制数) | D. | 57(十六制数) |
6.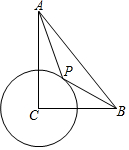 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,则AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,则AP+$\frac{1}{2}$BP的最小值为( )
 如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,则AP+$\frac{1}{2}$BP的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,则AP+$\frac{1}{2}$BP的最小值为( )| A. | $\sqrt{37}$ | B. | 6 | C. | 2 $\sqrt{17}$ | D. | 4 |

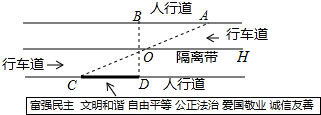 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下,如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC,BD相交于O,OD⊥CD垂足为D.已知AB=20米.根据上述信息,标语CD的长度为20m.
杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下,如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC,BD相交于O,OD⊥CD垂足为D.已知AB=20米.根据上述信息,标语CD的长度为20m.