题目内容
5.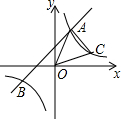 如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的坐标
如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的坐标为(1,m).
(1)求反比例函数y=$\frac{k}{x}$的表达式;
(2)点C(n,1)在反比例函数y=$\frac{k}{x}$的图象上,求△AOC的面积.
分析 (1)先求得A的坐标,然后利用待定系数法即可求得反比例函数y=$\frac{k}{x}$的表达式;
(2)把C(n,1)代入(1)求得的解析式求得C的坐标,过A作AD⊥x轴于D,过C作CE⊥x轴于E.根据S△AOC=S△AOD+S四边形ADEC-S△OCE,代入数值即可求得△AOC的面积.
解答 解:(1)∵点A(1,m)在一次函数y=x+2的图象上,
∴m=3.
∴点A的坐标为(1,3).
∵点A(1,3)在反比例函数y=$\frac{k}{x}$的图象上,
∴k=3.
∴反比例函数y=$\frac{k}{x}$的表达式为y=$\frac{3}{x}$. 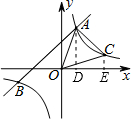 (2)∵点C(n,1)在反比例函数y=$\frac{3}{x}$的图象上,
(2)∵点C(n,1)在反比例函数y=$\frac{3}{x}$的图象上,
∴n=3.
∴C(3,1).
∵A(1,3).
如图,过A作AD⊥x轴于D,过C作CE⊥x轴于E.
则S△AOC=S△AOD+S四边形ADEC-S△OCE=
=$\frac{1}{2}$×1×3+$\frac{1}{2}$×(1+3)×(3-1)-$\frac{1}{2}$×3×1
=4.
点评 本题考查了反比例函数和一次函数的交点问题,待定系数法求反比例函数的解析式,反比例函数和一次函数图象上点的坐标特征,三角形的面积等知识.利用数形结合是解题的关键.

练习册系列答案
相关题目
13.已知不等式组$\left\{\begin{array}{l}{x-3(x-2)<a}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$仅有2个整数解,那么a的取值范围是( )
| A. | a≥2 | B. | a<4 | C. | 2≤a<4 | D. | 2<a≤4 |
10.已知实数a<0,则下列事件中是必然事件的是( )
| A. | 3a>0 | B. | a-3<0 | C. | a+3<0 | D. | a3>0 |
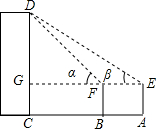 某数学小组用高为1.2米的仪器测量一教学楼的高CD,如图,距CD一定距离的A处,用仪器测得教学楼顶部D的仰角为β,再在A与C之间选一点B,由B处测出教学楼顶部D的仰角为α,测得A、B之间的距离为4米,若tanα=1.6,tanβ=1.2,则他们能求出教学楼的高吗?
某数学小组用高为1.2米的仪器测量一教学楼的高CD,如图,距CD一定距离的A处,用仪器测得教学楼顶部D的仰角为β,再在A与C之间选一点B,由B处测出教学楼顶部D的仰角为α,测得A、B之间的距离为4米,若tanα=1.6,tanβ=1.2,则他们能求出教学楼的高吗? 如图,?ABCD的顶点A、C、D都在⊙O上,AB与⊙O相切于点A,BC与⊙O交于点E,设∠OCD=α,∠BAD=β.
如图,?ABCD的顶点A、C、D都在⊙O上,AB与⊙O相切于点A,BC与⊙O交于点E,设∠OCD=α,∠BAD=β.