题目内容
17.点(1,y1)、(2,y2)都在一次函数y=kx+b(k>0)的图象上,则y1<y2(填“>”或“=”或“<”).分析 先根据k>0判断出函数的增减性,再由两点横坐标的值即可得出结论.
解答 解:∵一次函数y=kx+b中,k>0,
∴函数图象经过一三象限,y随x的增大而增大.
∵1<2,
∴y1<y2.
故答案为:<.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
8.我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( )
| A. | 2.5×10-5 | B. | 2.5×105 | C. | 2.5×10-6 | D. | 2.5×106 |
12.给出四个数0,$\sqrt{3}$,π,-1,其中最小的是( )
| A. | 0 | B. | $\sqrt{3}$ | C. | π | D. | -1 |
2.甲、乙两名同学在参加体育中考前各作了5次投掷实心球的测试,甲、乙所测得的成绩的平均数相同,且甲、乙成绩的方差分别为0.62、0.72,那么( )
| A. | 甲、乙成绩一样稳定 | B. | 甲成绩更稳定 | ||
| C. | 乙成绩更稳定 | D. | 不能确定谁的成绩更稳定 |
20.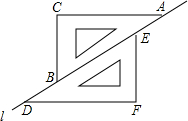 如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
 如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )| A. | BD=AE | B. | CB=BF | C. | BE⊥CF | D. | BA平分∠CBF |
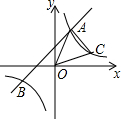 如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的坐标
如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的坐标