题目内容
8. 如图,?ABCD的顶点A、C、D都在⊙O上,AB与⊙O相切于点A,BC与⊙O交于点E,设∠OCD=α,∠BAD=β.
如图,?ABCD的顶点A、C、D都在⊙O上,AB与⊙O相切于点A,BC与⊙O交于点E,设∠OCD=α,∠BAD=β.(1)求证:AB=AE;
(2)试探究α与β之间的数量关系.
分析 (1)先证明∠CED=∠ADE,推出$\widehat{AE}$=$\widehat{CD}$,推出AE=CD,由此即可证明.
(2)延长AO交CD于F,由β=90°+∠OAD,∠OAD=$\frac{1}{2}$∠FOD,∠FOD=∠FOC=90°-α,由此即可解决问题.
解答 (1)证明:连接DE.
∵四边形ABCD是平行四边形,
∴BC∥AD,AB=CD,
∴∠CED=∠ADE,
∴$\widehat{AE}$=$\widehat{CD}$,
∴AE=CD,
∴AB=AE.
(2)延长AO交CD于F,
∵AB是⊙O切线,
∴AB⊥AF,
∵AB∥CD,
∴AF⊥CD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠COF=∠DOF=90°-α,
∵∠OAD=∠ODA,
∴$∠OAD=\frac{1}{2}$((90°-α),
∴β=90°+$\frac{1}{2}$(90°-α)=135°-$\frac{1}{2}$α.
点评 本题考查切线的性质、平行四边形的性质、圆的有关知识、垂径定理等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.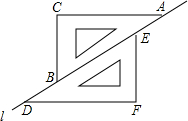 如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
 如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )| A. | BD=AE | B. | CB=BF | C. | BE⊥CF | D. | BA平分∠CBF |
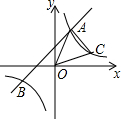 如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的坐标
如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的坐标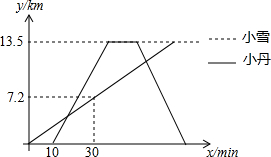 小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.
小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.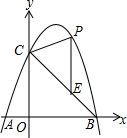 如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象与y轴交于点C(0,8),与x轴交于A,B两点,其中A(-2,0),B(6,0).
如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象与y轴交于点C(0,8),与x轴交于A,B两点,其中A(-2,0),B(6,0). 如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.