题目内容
13.已知不等式组$\left\{\begin{array}{l}{x-3(x-2)<a}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$仅有2个整数解,那么a的取值范围是( )| A. | a≥2 | B. | a<4 | C. | 2≤a<4 | D. | 2<a≤4 |
分析 首先解不等式组确定不等式组的解集,然后根据不等式组仅有2个整数解即可得到关于a的不等式组,求得a的值.
解答 解:$\left\{\begin{array}{l}{x-3(x-2)<a①}\\{\frac{1+2x}{3}>x-1②}\end{array}\right.$,
解①得:x>3-$\frac{1}{2}$a,
解②得:x<4,
则不等式组的解集是:3-$\frac{1}{2}$a<x<4.
不等式组仅有2个整数解,则是2,3.
则1≤3-$\frac{1}{2}a$<2.
解得:2<a≤4.
故选D.
点评 本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
4.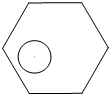 半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
 半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )| A. | a2(2$\sqrt{3}$-aπ) | B. | r2(2π-$\sqrt{3}$) | C. | a2r2(2$\sqrt{3}$-π) | D. | r2(2$\sqrt{3}$-π) |
1.某班数学兴趣小组收集了本市4月份30天的日最高气温的数据,经过统计分析获得了两条信息和一个统计表(天数为正整数).
信息1:4月份日最高气温的中位数是15.5℃;
信息2:4月份日最高气温的众数是17℃.
4月份日最高气温统计表
请根据上述信息求x,y,z的值.
信息1:4月份日最高气温的中位数是15.5℃;
信息2:4月份日最高气温的众数是17℃.
4月份日最高气温统计表
| 气温℃ | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 天数/天 | 2 | 3 | x | 5 | 4 | y | z | 3 | 2 | 3 |
8.我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( )
| A. | 2.5×10-5 | B. | 2.5×105 | C. | 2.5×10-6 | D. | 2.5×106 |
2.甲、乙两名同学在参加体育中考前各作了5次投掷实心球的测试,甲、乙所测得的成绩的平均数相同,且甲、乙成绩的方差分别为0.62、0.72,那么( )
| A. | 甲、乙成绩一样稳定 | B. | 甲成绩更稳定 | ||
| C. | 乙成绩更稳定 | D. | 不能确定谁的成绩更稳定 |
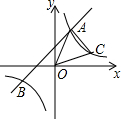 如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的坐标
如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的坐标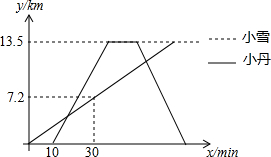 小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.
小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.