题目内容
8.已知$\frac{x}{3}=\frac{y}{7}=\frac{z}{5}$,设A=$\frac{y}{x+y+z}$,B=$\frac{x+y}{x}$,C=$\frac{x-y+z}{z}$,试比较它们大小.分析 根据题中等式表示出x,y,z,进而求出A,B,C的值,比较即可.
解答 解:由$\frac{x}{3}$=$\frac{y}{7}$=$\frac{z}{5}$=k,得到x=3k,y=7k,z=5k,
∴A=$\frac{7k}{3k+7k+5k}$=$\frac{7}{15}$,B=$\frac{3k+7k}{3k}$=$\frac{10}{3}$,C=$\frac{3k-7k+5k}{5k}$=$\frac{3}{5}$,
则A<C<B.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13.等腰三角形两边长分别是5和7,则该三角形周长为( )
| A. | 17 | B. | 19 | C. | 17或19 | D. | 无法确定 |
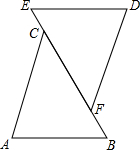 如图,已知△ABC≌△DEF,∠A=70°,∠B=60°,BF=2.
如图,已知△ABC≌△DEF,∠A=70°,∠B=60°,BF=2. 如图,Rt△ABC中,BC=11cm,AC=7cm,点M从点B出发沿BC匀速向点C运动,点N从点C出发沿CA匀速向点A运动.
如图,Rt△ABC中,BC=11cm,AC=7cm,点M从点B出发沿BC匀速向点C运动,点N从点C出发沿CA匀速向点A运动. 如图,△ABC与△DEF是中心对称图形,A,B,C的对应点分别是D,E,F,小明画好点D后有事走开了,请你帮他把△DEF画完整.
如图,△ABC与△DEF是中心对称图形,A,B,C的对应点分别是D,E,F,小明画好点D后有事走开了,请你帮他把△DEF画完整. 如图,C为BE上一点,AB=AC,BE=CD.
如图,C为BE上一点,AB=AC,BE=CD.