题目内容
13.等腰三角形两边长分别是5和7,则该三角形周长为( )| A. | 17 | B. | 19 | C. | 17或19 | D. | 无法确定 |
分析 腰长是5或7,两种情况都可能出现,因而分两种情况确定三角形的边长,即可求出周长.
解答 解:三角形的腰长是5时,三角形的三边长是:5,5,7,则周长是:5+5+7=17;
当三角形的腰长是7时,三角形的三边长是:5,7,7,则周长是:5+7+7=19.
故选:C.
点评 考查了等腰三角形的性质和三角形三边关系,本题从边的方面考查三角形,涉及分类讨论的思想方法.求三角形的周长,不能盲目地将三边长相加起来,而应养成检验三边长能否组成三角形的好习惯,把不符合题意的舍去.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
5.二次函数y=ax2+bx+c图象上部分点的对应值如下表
则使y<0的x的取值范围为( )
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | 0 | -4 | -6 | -6 | -4 | 0 | 6 |
| A. | x<0 | B. | x>$\frac{1}{2}$ | C. | -2<x<3 | D. | x<-2或x>3 |
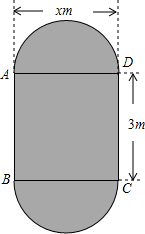 如图.在矩形ABCD中,AD=xm,CD=3m,以AD、BC为直径在矩形外侧分别作两个半圆,设图中阴影部分的面积为ym2,求 y(m2)与x(m)之间的函数关系式.
如图.在矩形ABCD中,AD=xm,CD=3m,以AD、BC为直径在矩形外侧分别作两个半圆,设图中阴影部分的面积为ym2,求 y(m2)与x(m)之间的函数关系式.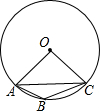 如图,点A、B、C在圆O上,AC是圆O的内接正六边形的一边,BC是圆的内接正八边形的一边,AB能否成为圆O的内接正n边形的一边?如果能,求出n的值;如果不能,请说明理由.
如图,点A、B、C在圆O上,AC是圆O的内接正六边形的一边,BC是圆的内接正八边形的一边,AB能否成为圆O的内接正n边形的一边?如果能,求出n的值;如果不能,请说明理由.