题目内容
20.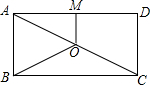 如图,O是矩形ABCD对角线AC的中点,M是AD的中点,若BC=8,OB=5,则OM的长为( )
如图,O是矩形ABCD对角线AC的中点,M是AD的中点,若BC=8,OB=5,则OM的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 首先由O是矩形ABCD对角线AC的中点,可求得AC的长,然后由勾股定理求得AB的长,即CD的长,又由M是AD的中点,可得OM是△ACD的中位线,继而求得答案.
解答 解:∵O是矩形ABCD对角线AC的中点,OB=5,
∴AC=2OB=10,
∴CD=AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵M是AD的中点,
∴OM=$\frac{1}{2}$CD=3.
故选C.
点评 此题考查了矩形的性质、直角三角形的性质以及三角形中位线的性质.注意利用直角三角形斜边上的中线等于斜边的一半,求得AC的长是关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
10.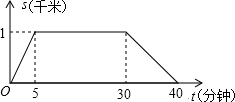 某天早晨,小明去体育馆晨练,如图是他离家的距离S(千米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是( )
某天早晨,小明去体育馆晨练,如图是他离家的距离S(千米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是( )
 某天早晨,小明去体育馆晨练,如图是他离家的距离S(千米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是( )
某天早晨,小明去体育馆晨练,如图是他离家的距离S(千米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是( )| A. | 小明去时所用的时间多于回家所用的时间 | |
| B. | 小明在体育馆锻炼了30分钟 | |
| C. | 小明去时的速度大于回家的速度 | |
| D. | 小明去时走上坡路,回家时走下坡路 |
8.已知y与x成正比例,并且x=1时,y=8,那么y与x之间的函数关系式为( )
| A. | y=8x | B. | y=2x | C. | y=6x | D. | y=5x |
15.记录一个病人体温变化情况选用的统计图是( )
| A. | 折线统计图 | B. | 扇形统计图 | C. | 条形统计图 | D. | 以上都不行 |
12.马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于830°,则该多边形的边数是( )
| A. | 7 | B. | 8 | C. | 7或8 | D. | 无法确定 |
10.如果关于x的一元二次方程2x2-x+k=0有两个实数根,那么k的取值范围是( )
| A. | k≥$\frac{1}{8}$ | B. | k≤$\frac{1}{8}$ | C. | k≥-$\frac{1}{8}$ | D. | k≤-$\frac{1}{8}$ |
 如图,将平行四边形ABCD的边AB延长至点E,使BE=AB,连接DE,EC,DE,交BC于点O.
如图,将平行四边形ABCD的边AB延长至点E,使BE=AB,连接DE,EC,DE,交BC于点O.