题目内容
11. 如图,将平行四边形ABCD的边AB延长至点E,使BE=AB,连接DE,EC,DE,交BC于点O.
如图,将平行四边形ABCD的边AB延长至点E,使BE=AB,连接DE,EC,DE,交BC于点O.(1)求证:△ABD≌△BEC;
(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.
分析 (1)由平行四边形ABCD,易得四边形BECD为平行四边形,然后由SSS推出两三角形全等即可;
(2)由(1),易证得BC=ED,即可证得四边形BECD是矩形.
解答 证明:(1)在平行四边形ABCD中,AD=BC,AB=CD,AB∥CD,则BE∥CD.
又∵AB=BE,
∴BE=DC,
∴四边形BECD为平行四边形,
∴BD=EC.
∴在△ABD与△BEC中,
$\left\{\begin{array}{l}{AB=BE}\\{BD=EC}\\{AD=BC}\end{array}\right.$,
∴△ABD≌△BEC(SSS);
(2)由(1)知,四边形BECD为平行四边形,则OD=OE,OC=OB.
∵四边形ABCD为平行四边形,
∴∠A=∠BCD,即∠A=∠OCD.
又∵∠BOD=2∠A,∠BOD=∠OCD+∠ODC,
∴∠OCD=∠ODC,
∴OC=OD,
∴OC+OB=OD+OE,即BC=ED,
∴平行四边形BECD为矩形.
点评 本题考查了平行四边形的性质和判定,矩形的判定,平行线的性质,全等三角形的性质和判定以及三角形的外角性质等知识.注意证得四边形BECD为平行四边形是关键.

练习册系列答案
相关题目
6.已知$\left\{\begin{array}{l}{x=2+t}\\{y=2-t}\end{array}\right.$,则用含x的式子表示y,应是( )
| A. | x=-y+4 | B. | y=4x | C. | y=-x+4 | D. | y=x-4 |
16.在有25名男生和20名女生的班级中,随机抽取一名学生做代表,则下列说法正确的是( )
| A. | 男、女生做代表的可能性一样大 | |
| B. | 男生做代表的可能性大 | |
| C. | 女生做代表的可能性大 | |
| D. | 男、女生做代表的可能性大小不能确定 |
3. 如图,已知∠AEF=∠EGH,AB∥CD,则下列判断中不正确的是( )
如图,已知∠AEF=∠EGH,AB∥CD,则下列判断中不正确的是( )
 如图,已知∠AEF=∠EGH,AB∥CD,则下列判断中不正确的是( )
如图,已知∠AEF=∠EGH,AB∥CD,则下列判断中不正确的是( )| A. | ∠AEF=∠EFD | B. | AB∥GH | C. | ∠BEF=∠EGH | D. | GH∥CD |
1.已知P=60×104×20,则P可用科学记数法表示为( )
| A. | 1.2×108 | B. | 1.2×107 | C. | 1.2×106 | D. | 12×106 |
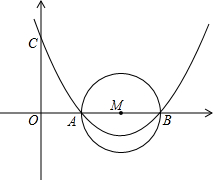 如图所示,已知M的坐标为(4,0),以M为圆心,以2为半径的圆交x轴于点A、B,抛物线y=$\frac{1}{6}$x2+bx+c过A、B两点且与y轴交于点C.
如图所示,已知M的坐标为(4,0),以M为圆心,以2为半径的圆交x轴于点A、B,抛物线y=$\frac{1}{6}$x2+bx+c过A、B两点且与y轴交于点C.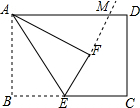 如图,在矩形ABCD中的AB边长为6,BC边长为9,E为BC上一点,且CE=2BE,将△ABE翻折得到△AFE,延长EF交AD边于点M,则线段DM的长度为$\frac{3}{2}$.
如图,在矩形ABCD中的AB边长为6,BC边长为9,E为BC上一点,且CE=2BE,将△ABE翻折得到△AFE,延长EF交AD边于点M,则线段DM的长度为$\frac{3}{2}$.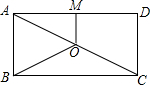 如图,O是矩形ABCD对角线AC的中点,M是AD的中点,若BC=8,OB=5,则OM的长为( )
如图,O是矩形ABCD对角线AC的中点,M是AD的中点,若BC=8,OB=5,则OM的长为( )