题目内容
9.已知反比例函数$y=\frac{k}{x}$,其中k>-2,且k≠0,1≤x≤2.(1)若y随x的增大而增大,则k的取值范围是-2<k<0;
(2)若该函数的最大值与最小值的差是1,求k的值.
分析 (1)根据函数的单调性结合反比例函数的性质即可得出k<0,再由k的取值范围即可得出结论;
(2)分反比例函数单减和单增两种情况考虑,根据最大值与最小值的差是1,可得出关于k的一元一次方程,解方程即可得出结论.
解答 解:(1)∵y随x的增大而增大,
∴k<0,
∵k>-2,且k≠0,
∴-2<k<0.
故答案为:-2<k<0.
(2)当-2<k<0时,在1≤x≤2范围内,y随x的增大而增大,
∴$\frac{k}{2}-k=1$,
解得k=-2,不合题意,舍去;
当k>0时,在1≤x≤2范围内,y随x的增大而减小,
∴$k-\frac{k}{2}=1$,
解得k=2.
综上所述:若该函数的最大值与最小值的差是1,k的值为2.
点评 本题考查了反比例函数的性质以及解一元一次方程,解题的关键是:(1)根据反比例函数的性质找出k的取值范围;(2)分情况考虑,找出关于k的方程.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数系数k结合反比例函数的性质找出函数的单调性是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.为支援云南地震灾区,中央电视台晚举办了爱的奉献赈灾晚会,晚会现场捐款达1514000000元.1514000000用科学记数法表示正确的是( )
| A. | 1.514×106 | B. | 15.14×109 | C. | 1.514×109 | D. | 1.514×1010 |
14.某计算器每个定价80元,若购买不超过20个,则按原价付款:若一次购买超过20个,则超过部分按七折付款.设一次购买数量为x(x>20)个,付款金额为y元,则y与x之间的表达式为( )
| A. | y=0.7×80(x-20)+80×20 | B. | y=0.7x+80(x-10) | ||
| C. | y=0.7×80•x | D. | y=0.7×80(x-10) |
1.已知P=60×104×20,则P可用科学记数法表示为( )
| A. | 1.2×108 | B. | 1.2×107 | C. | 1.2×106 | D. | 12×106 |
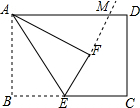 如图,在矩形ABCD中的AB边长为6,BC边长为9,E为BC上一点,且CE=2BE,将△ABE翻折得到△AFE,延长EF交AD边于点M,则线段DM的长度为$\frac{3}{2}$.
如图,在矩形ABCD中的AB边长为6,BC边长为9,E为BC上一点,且CE=2BE,将△ABE翻折得到△AFE,延长EF交AD边于点M,则线段DM的长度为$\frac{3}{2}$.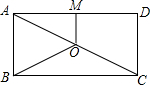 如图,O是矩形ABCD对角线AC的中点,M是AD的中点,若BC=8,OB=5,则OM的长为( )
如图,O是矩形ABCD对角线AC的中点,M是AD的中点,若BC=8,OB=5,则OM的长为( )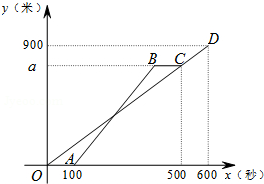 甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.
甲、乙两人从学校出发,沿相同的线路跑向体育馆,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向体育馆,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.