题目内容
10.如果关于x的一元二次方程2x2-x+k=0有两个实数根,那么k的取值范围是( )| A. | k≥$\frac{1}{8}$ | B. | k≤$\frac{1}{8}$ | C. | k≥-$\frac{1}{8}$ | D. | k≤-$\frac{1}{8}$ |
分析 由于方程有实数根,则根的判别式△≥0,由此建立关于k的不等式,解不等式即可求得k的取值范围.
解答 解:∵关于x的一元二次方程2x2-x+k=0有两个实数根,
∴△=b2-4ac=1-4×2k=1-8k≥0,
∴k≤$\frac{1}{8}$.
故选B.
点评 此题考查了根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
1.已知P=60×104×20,则P可用科学记数法表示为( )
| A. | 1.2×108 | B. | 1.2×107 | C. | 1.2×106 | D. | 12×106 |
 如图,O是矩形ABCD对角线AC的中点,M是AD的中点,若BC=8,OB=5,则OM的长为( )
如图,O是矩形ABCD对角线AC的中点,M是AD的中点,若BC=8,OB=5,则OM的长为( )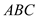 的顶点
的顶点 的坐标为
的坐标为 ,
,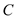 的坐标为
的坐标为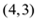 ,直角顶点
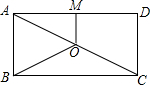
,直角顶点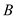 在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.
在第四象限,线段AC与x轴交于点D.将线段DC绕点D逆时针旋转90°至DE.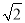 个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.
个单位的速度运动到E后停止.当点F的坐标是多少时,是否存在点M在整个运动过程中用时最少?若存在,请求出点F的坐标;若不存在,请说明理由.